フィヨルドブートキャンプを辞める。という話

本日をもってフィヨルドブートキャンプを終了することになりました。
はじめに断っておくと、フィヨルドブートキャンプは素敵なプログラムです。私自身も後ろ向きな理由で辞めるわけではありません。
メンターの駒形さん、町田さんの御好意で、初訪問で辞めます宣言したフィヨルドオフィスから、コーヒーにEuRuKoお土産のお菓子までご馳走になりながらこのブログを綴っております(なんと厚かましいやつ!)
なぜフィヨルドブートキャンプに参加していたのか
私がどんなキャリアを歩んできたのかは、下記リンク先の記事
を読む必要がないように、ざっくり説明すると
- 汎用機系SEやってたけど、キャリア形成する上でかなりまずい状態なのを自覚しており、「特定の会社に依存せず、どこへ行っても通用する力をつけたい」と考え、データアナリストに転身
- したつもりだったが、実態はデータエンジニアとしてデータマネジメント業務。と、言いたい孤独なデータマート拵えおじさんと化してしまい、ひたすらに危機感を募らせていく(やるべきことはやってきましたが。)
- (今年の初旬からそれまで以上に業務時間外での学習時間を必死で確保、さまざまな会社のミートアップやカジュアル面談に行ったり、誘っていただければ応募してみたりを数ヶ月続けました)
select-from-where.hatenablog.com
select-from-where.hatenablog.com
そんな活動の末、自分の目指すデータアナリストとしてのキャリアの方向性に迷いや悩みを抱えるに至りました。
毎日モヤモヤした気持ちを抱えながら過ごしていたところ、フィヨルドブートキャンプに出会い、いつも気にかけてくれ、たくさんのアドバイスをくれる友人(エンジニアとして大活躍中)の強い勧めもあって参加を検討し始めました。
私自身も「なにこのサービスすごい...しかも学費いらんって最高やん...」と思うにいたり、komagataさんのこのブログ記事を読んで参加を決意。
下記の応募フォームに必要事項を記入して送信。無事、参加させていただくことが決まったのでした。
エンジニアリングを体系的に学び、プログラマ・エンジニアとしてサービス開発の現場を経験した後、まだ未練が残っていればデータエンジニアリング/マネジメント/アナリティクスの領域に戻るのは割と現実的なキャリアプランのように思えました。サービス開発の現場を知っている、自分で実装できるスキルがあるのは、その後のキャリアを強化してくれそうだと考えていました。
年齢的にもじっくり学びなおす最後のチャンスかもしれない。ブートキャンプを終えた後のキャリアに対するワクワク感は非常に大きく、10月以降は学習に専念するため在職中の会社に退職を願い出ました。
フィヨルドブートキャンプに期待していたこと
「自分で開発したサービスを持って転職活動をする」というブートキャンプのコンセプトがもっとも魅力を感じた点なのですが、他には以下のようなことを期待して参加していました。
- 事業会社に転職すること(組織づくりや風土・仕組みづくりにも関心があるため、これ以上クライアントワークはしたくない)
- Webサービス開発のエンジニアリングを、メンターのフォローを受けながら体系的にじっくりと学ぶこと
- プログラマ、エンジニアとしての心構えやカルチャーを体感し、コミュニティに属すること
実際に自分が学習を進めながら受けたフォローや、他の参加者の方の様子を見ていて、最後までやり切ることができれば、2, 3に関しては確実に期待に沿う結果が得られていたと思います。
なぜフィヨルドブートキャンプを辞めるのか
ブートキャンプ参加時点で選考を残していた1社に、データアナリストとしての転職が決まりました。
選考に通っても落ちてもブートキャンプに邁進するつもりだったので身構えすぎず(めっちゃくちゃ緊張はしましたが)、ありのままの経験や仕事に対する考え方を話した結果、カルチャーへのフィットや人となりを重視してくれる会社だったため、内定をいただくことができました。
内定承諾期限間際まで悩みましたが、ビジョン・プロダクト・人が魅力的だと感じており、逃してはならないチャンスのように思えました。プログラマ・エンジニアへのキャリアチェンジではなく、現職で得た経験やスキルを活かしたキャリアアップの道を選ぶことに決め、ブートキャンプの終了を申し出るため、本日初めてのフィヨルドオフィスに足を運びました。
フィヨルドブートキャンプに参加して感じたこと
このブートキャンプの(技術面での)核心に近いプラクティスであるはずの、Ruby, Ruby on Railsに到達する前、かなり初期に近い段階で辞めてしまうため、浅い体験談になってはしまいますが...
「プログラマーとして就職を希望する方のための就職支援サービス」であるだけに、学べることは技術的なスキルだけはないと感じました。
どこで誰と働くときでも必須となる「問題解決能力・判断力」、エンジニアとしてキャリアを構築するために欠かせない「学び続ける力」を養うことができるカリキュラムになっていると思います。
参加を迷ってこの記事に辿り着いた方へ
まずはホームページに記載されている内容をよく読み込み、問い合わせフォームからコンタクトを取って見ることをお勧めします。下記も参考にしてみてください。
1.Web業界のカルチャーに触れられる
プラクティスの初期、学習の準備「SNSの登録」でも説かれているのですが、人と繋がりを作ること、アウトプットを公にしておくことは「機会を得る可能性を高める」と言う意味でとても大切です。これまでに出会った優秀であると評価されているエンジニアの方々は総じて同じようなことをアドバイスしてくれます。
学校や一つの会社しか知らない閉じた世界に生きていたり、ただインターネットに繋がっているだけでは気づくことが難しいWeb業界の独特な文化を、その世界に身を投じる前から体感することができると思います。
2.人との繋がり
そもそも私がブートキャンプに参加した決め手の一つは、フィヨルドブートキャンプを卒業した優秀なエンジニアの方との遠い縁です。
信頼している友人が「尊敬しているし信頼しているエンジニアの方」がフィヨルドの関係者で、ブートキャンプは明確な学ぶ動機があるならオススメできると言っている(←ややこしい)と言う事実は、受講を決める上で大きく背中を押してくれました。
このような細い縁が、現実に繋がっていきやすいのがこの業界だと思います。
また、フィヨルドブートキャンプにはメンターのお二方に限らず、困っている人がいればアドバイスを送ったり、サポートをしてくれる人が何人も存在します。そこで披露された知見は、日報やWikiにナレッジとして蓄積されています。
得られるのは直接的なサポートだけではありません。「今日もあの人は時間をかけて丁寧に学んでいるな」とか、「この方はそう言うことにモチベーションがあって今頑張っているのか」とか、「めちゃくちゃわかりやすい説明する人だな」とか、「素敵なブログ書く人だな」といったことが日報やブログ、twitterで垣間見れるのは、たくさんのプラクティスをこなして行く上で大変な心の支えになるのではないかと思います。
3.やはり体系的に学んでおくことは大事(と言うか安心)
私は小心者なので、知識を体系的に学んでから手を動かすことが大事で、長期的に見ると安心感を得やすいです。そのためフィヨルドのカリキュラムにフィットしていた気がします。
よくはわからないが動くものにはなっているようなシステムは、職場での責任が大きくなるほどに距離を置きたい悩ましい存在になっていきます。
基礎から体系的に学んでいれば、仕組みを紐解いて技術的負債をリファクタリングできるのかもしれない...と思う日はいずれ来るものです。
フィヨルドブートキャンプで学べる技術は下記リンク先の記事を参考にしてください。
4.効率よく”教わりたい”人にはオススメできない
このブートキャンプは ”学ぶための” 場所であり、”教わるための” 場所ではないことを認識しておく必要があります。
提携先の企業との信頼関係で成り立っているサービスのため、就職させるためではなく、就職先で活躍させることを目指して作り込まれたカリキュラムになっています。
意図的に学習コストを下げて挫折しにくくいようにし、楽しく最後まで進められるように作られたプラクティスは序盤でもありませんでしたし、おそらくその先もありません。
効率よく最短(のように見える)ルートで教わりたい人*1は、別のブートキャンプや学習方法を検討したほうが良さそうです。
5.それほど覚悟が決まっていない人はProgate
今は特に独学で学んだりしていないけど、今の環境が不満だし将来が不安。Webエンジニアの職場環境とか待遇はいいらしい*2、ブートキャンプで教えてもらえればやれそう、とか思っていたらちょっと待った!です。
在職中だと学習時間の確保にストレスを伴うセルフマネジメントが必要になってくる環境の人の方が多いと思います。参加を決める前にProgateを活用して、HTML, CSS, Command Line, Git, Ruby, Ruby on Railsまでを、休日に集中してやるか、平日も頑張るのか、コンスタントに消化することにトライしてみると良さそうです(最近の受講者の方はこのルートを辿っている人がちらほらいるはず)。
Progateでの学習を計画を立てて実行できれば大丈夫です。自ら学ぶ姿勢があれば、困った時はメンターの方、アドバイザーの方、親切な受講者の方が助けになってくれます。何より、他の受講者の学生さんや社会人の方が懸命に学んでいる様子はとても刺激になりますよ。
これからのキャリアについて
ここしっかり書けよ!って感じですが、これまでの章を書いたり消したり推敲を繰り返したので(話の抽象度高くしすぎたかも)息切れしました。笑
データアナリストとして戦力になるには、一人前のRailsエンジニアになるのと同じくらい、まだまだたくさんの学習が必要です。これまでのキャリアで培った組織課題を見つける力やそれに対する取り組み、データマネジメントスキル、折衝力、コミュニケーションスキルを活かして組織貢献しつつ、貪欲に学んで成果を上げられる人材に成長したいものです。
その傍ら、小さなプロダクトを作って公開できるように、Railsの学習はフィヨルドブートキャンプのカリキュラムを参考にゆっくりと続けていこうと思います。
Web業界の素敵なところは、オープンでgiveを惜しまない人が多いところです。 今のところ、私はまだまだ人にgiveしてもらいっぱなし。一端のデータアナリストになって、一緒に働く人に限らず様々な人に還元して行けるような人間になりたいと思います。
次の会社はRubyとの繋がりも深い会社なので、なんとかFjordとの架け橋を作るきっかけになれるといいな、などと思っています。
【黒い画面】Terminal使うなら、最低限このくらいまで
ここに「Fjord Bootcampに参加する」という記事を埋め込む予定(だった)。
さて、Fjord Bootcampを少しづつ進めているが、本日はその課題。
Webデザイナーの為の「本当は怖くない」“黒い画面”入門をPart.09まで読み進めます。
(タイトル:ターミナル触るなら、このくらいは知っとくべきだったなと思ったので、真面目に)
■ 意識すること
Terminalはそれなりに使っているけど、これまではやりたいことをできればいい感覚だったので課題感がある。この辺りはできる限り解消していきたいところ。
- いろいろ用語が怪しい
(ちゃんとしたエンジニアさんと話すと??あ、それのことですか...がよくある) - "おまじない" 扱いして理解していないコマンドがある
(export, chmod)
■ コマンド群
知らなかった、使ったことない
- env (ENVironment)
環境変数を表示、変更する - man (MANual)
各コマンドのマニュアルを確認できる - open
ファイルやフォルダを開く - chown (CHange OWNer)
ファイルやグループの所有者を変更する - chsh
使用するシェルを変更する
- env (ENVironment)
おまじない化していた
よく使う、使ったことがある
■ やってみた
echoで環境変数を確認する
$ echo $PATH /Users/s_f_w/.rbenv/shims:/Users/s_f_w/anaconda/bin:/usr/bin:/bin:/usr/sbin:/sbin:/usr/local/bin $ echo $USER s_f_w $ echo $HOME /Users/s_f_w
envで環境変数を確認する
$ env TERM_PROGRAM=Apple_Terminal TERM=xterm-256color SHELL=/bin/bash -- 略 -- USER=s_f_w -- 略 -- PATH=/Users/s_f_w/.rbenv/shims:/Users/s_f_w/anaconda/bin:/usr/bin:/bin:/usr/sbin:/sbin:/usr/local/bin PWD=/bin LANG=ja_JP.UTF-8 -- 略 -- HOME=/Users/s_f_w -- 略 --
saykanaで学習を促してくるコマンドを作成
注意:この後、OS再インストールするつもりなのでやりますが、一度通したパスを削除するの結構めんどくさいみたいです。この方法は簡単そうだった。
$ pwd /Users/s_f_w $ mkdir -p test_command/bin $ cd test_command/bin $ pwd /Users/s_f_w/test_command/bin $ vim wakeup_study #! /bin/sh saykana めわさめた? read -p "目は覚めましたか?(y or n) :" saykana きのうのふくしゅうわした? read -p "復習はしましたか?(y or n) :" saykana きょうのがくしゅうのじゅんびわできた? read -p "準備はできましたか?(y or n) :" saykana よろしい。はよやれ $ less wakeup_study $ chmod u+x wakeup_study $ wakeup_study $ export PATH=$PATH:/Users/s_f_w/test_command/bin $ echo $PATH /Users/s_f_w/.rbenv/shims:/Users/s_f_w/anaconda/bin:/usr/bin:/bin:/usr/sbin:/sbin:/usr/local/bin:/Users/s_f_w/test_command/bin
そして実行。
$ wakeup_study 目は覚めましたか?(y or n) :y 復習はしましたか?(y or n) :y 準備はできましたか?(y or n) :y ==> saykana 「よろしい。はよやれ」
やかましわ。でも大事なことですね(いい歳こいてバカみたい。)
■ Terminalに纏わる予備知識
- ホスト名 = コンピュータに付けた名前
- プロンプト = ターミナルを開くと出てくる"$"マークまでの部分
(カスタマイズできるらしい...!!!) - 環境変数 = ターミナル上で初めから定義されている変数
- bin = binary
- カレントワーキングディレクトリ = 今いるディレクトリ
- 相対パス = 今いるディレクトリから見たパス
- オプションの種類
- ショートネームオプション 例)"ls -l"
- ロングネームオプション 例)"ls -list"
- パッケージマネージャ = ソフトの依存関係をバージョンを考慮して管理してくれるシステム
- Homebrew
- Anaconda
- pip (Pip Installs Python)
- SDK (Software Development Kit) = ソフトウェアを作るために必要なものの詰め合わせ
- shebang = "#!"を指す。shellに対して、以降に記述したディレクトリに、ファイルの内容を処理するように命令する
- パスを通す = 環境変数にディレクトリを追加して、コマンドとして実行可能にすること
- 黒い画面
■ 感想
Kaggleに挑戦する - 与えられたデータの確認2
前回の続き。
select-from-where.hatenablog.com
挑戦する(したかった)コンペはこちら。
Recruit Restaurant Visitor Forecasting | Kaggle
最新のソースはGitHubで公開、随時更新していく。
今回は与えられたデータの確認2回目。
与えられたcsvデータどうしを結合して分析していきます。
8.Airリザーブの訪問データに予約データを結合
- キャンセル数はこのデータから把握することができない
# 訪問データを読み込み air_visit_df = pd.read_csv('Data/csv/air_visit_data.csv') air_visit_df.tail(3)
| air_store_id | visit_date | visitors | |
|---|---|---|---|
| 252105 | air_24e8414b9b07decb | 2017-04-20 | 7 |
| 252106 | air_24e8414b9b07decb | 2017-04-21 | 8 |
| 252107 | air_24e8414b9b07decb | 2017-04-22 | 5 |
# 予約データを日次に加工 air_reserve_df = pd.read_csv('Data/csv/air_reserve.csv') air_reserve_df['visit_datetime'] = air_reserve_df['visit_datetime'].str[:10] air_reserve_df = air_reserve_df.rename(columns={'visit_datetime': 'visit_date'}).drop('reserve_datetime',axis=1) air_reserve_df = air_reserve_df.groupby(['air_store_id','visit_date'])['reserve_visitors'].sum().reset_index() air_reserve_df.tail(3)
| air_store_id | visit_date | reserve_visitors | |
|---|---|---|---|
| 29827 | air_fea5dc9594450608 | 2017-04-28 | 3 |
| 29828 | air_fea5dc9594450608 | 2017-05-20 | 6 |
| 29829 | air_fee8dcf4d619598e | 2017-01-09 | 5 |
# 予測対象の店舗のみに絞り込む # サンプルデータを読み込んで、一意なstore_idを取り出し sample = pd.read_csv('Data/csv/sample_submission.csv') # 他のデータセットと形式を合わせておく sample_id = DataFrame(sample, columns=['air_store_id']) sample_id['air_store_id'] = sample.id.map(lambda x: '_'.join(x.split('_')[:-1])) sample_id = sample_id.drop_duplicates().reset_index(drop=True) sample_id.tail(3)
# 訪問データ を予測対象に絞り込み air_df = pd.merge(air_visit_df,sample_id,on=['air_store_id'],how='inner') air_df.tail(3)
| air_store_id | visit_date | visitors | |
|---|---|---|---|
| 250465 | air_24e8414b9b07decb | 2017-04-20 | 7 |
| 250466 | air_24e8414b9b07decb | 2017-04-21 | 8 |
| 250467 | air_24e8414b9b07decb | 2017-04-22 | 5 |
# 訪問データに予約データを結合 air_df = pd.merge(air_visit_df,air_reserve_df,on=['air_store_id','visit_date'],how='left') air_df.tail(3)
| air_store_id | visit_date | visitors | reserve_visitors | |
|---|---|---|---|---|
| 252105 | air_24e8414b9b07decb | 2017-04-20 | 7 | NaN |
| 252106 | air_24e8414b9b07decb | 2017-04-21 | 8 | NaN |
| 252107 | air_24e8414b9b07decb | 2017-04-22 | 5 | NaN |
air_df.describe(include='all')
| air_store_id | visit_date | visitors | reserve_visitors | |
|---|---|---|---|---|
| count | 252108 | 252108 | 252108.000000 | 28064.000000 |
| unique | 829 | 478 | NaN | NaN |
| top | air_5c817ef28f236bdf | 2017-03-17 | NaN | NaN |
| freq | 477 | 799 | NaN | NaN |
| mean | NaN | NaN | 20.973761 | 13.751283 |
| std | NaN | NaN | 16.757007 | 17.284799 |
| min | NaN | NaN | 1.000000 | 1.000000 |
| 25% | NaN | NaN | 9.000000 | 5.000000 |
| 50% | NaN | NaN | 17.000000 | 10.000000 |
| 75% | NaN | NaN | 29.000000 | 18.000000 |
| max | NaN | NaN | 877.000000 | 1633.000000 |
8–1.日次の訪問予定者数、訪問者数、予約訪問者率(訪問予定者数 / 訪問者数)
# 訪問データを日次で集計 air_df_daily = air_df.copy() air_df_daily['visit_date'] = air_df_daily.visit_date.map(lambda x: datetime.strptime(x,'%Y-%m-%d')) air_df_daily = air_df_daily.drop('air_store_id',axis=1) air_df_daily = air_df_daily.groupby(['visit_date'])['reserve_visitors','visitors'].sum().reset_index() air_df_daily.tail(3)
| visit_date | reserve_visitors | visitors | |
|---|---|---|---|
| 475 | 2017-04-20 | 1488.0 | 13990 |
| 476 | 2017-04-21 | 3413.0 | 19624 |
| 477 | 2017-04-22 | 2861.0 | 21245 |
# reserve_rate を追加して予約率を算出 air_df_daily['reserve_rate'] = air_df_daily['reserve_visitors'] / air_df_daily['visitors'] * 100 air_df_daily[air_df_daily['reserve_rate'] > 0].head(3)
| visit_date | reserve_visitors | visitors | reserve_rate | |
|---|---|---|---|---|
| 0 | 2016-01-01 | 17.0 | 1033 | 1.645692 |
| 1 | 2016-01-02 | 128.0 | 1764 | 7.256236 |
| 2 | 2016-01-03 | 53.0 | 2368 | 2.238176 |
air_df_daily.describe(include='all')
| visit_date | reserve_visitors | visitors | reserve_rate | |
|---|---|---|---|---|
| count | 478 | 392.000000 | 478.000000 | 392.000000 |
| unique | 478 | NaN | NaN | NaN |
| top | 2016-09-08 00:00:00 | NaN | NaN | NaN |
| freq | 1 | NaN | NaN | NaN |
| first | 2016-01-01 00:00:00 | NaN | NaN | NaN |
| last | 2017-04-22 00:00:00 | NaN | NaN | NaN |
| mean | NaN | 984.479592 | 11062.035565 | 8.140861 |
| std | NaN | 947.290374 | 5079.505034 | 4.490445 |
| min | NaN | 2.000000 | 1033.000000 | 0.010993 |
| 25% | NaN | 274.000000 | 5894.500000 | 5.103207 |
| 50% | NaN | 672.500000 | 11429.500000 | 8.117165 |
| 75% | NaN | 1341.000000 | 14286.000000 | 10.751376 |
| max | NaN | 4619.000000 | 23982.000000 | 21.465458 |
# 折れ線グラフで描画 line_height1 = air_df_daily.reserve_visitors.as_matrix() line_height2 = air_df_daily.visitors.as_matrix() line_height3 = air_df_daily.reserve_rate.as_matrix() left = air_df_daily.visit_date fig, ax1 = plt.subplots(figsize=(18, 10)) p1 = plt.plot(left, line_height1, color="deepskyblue") p2 = plt.plot(left, line_height2, color="navy") ax1.set_ylabel('Num of people') ax2 = ax1.twinx() p3 = ax2.plot(left, line_height3, color="red") ax2.set_ylabel('Reserve Rate') ax2.set_ylim(0, 50) plt.legend((p1[0], p2[0], p3[0]), ("reserve", "visit", "reserve_rate"), loc='upper right', bbox_to_anchor=(0.7, 0.5, 0.5, 0.5)) plt.title("daily_visitors") plt.xlabel("visit_date") plt.grid(True)
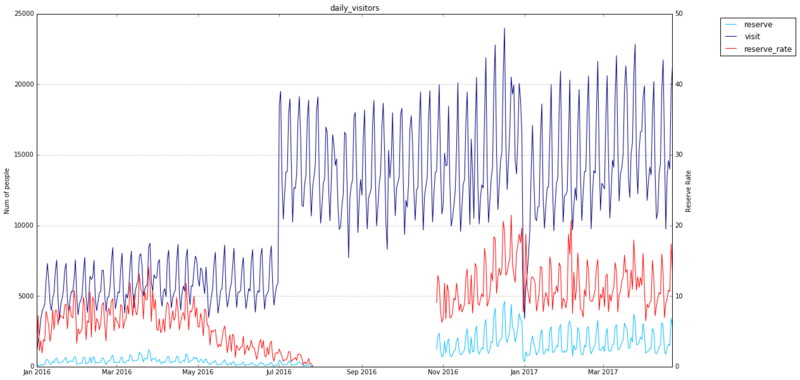
8–2.気づき
訪問データありに限ると、予約データが欠損している期間がある
- 2016年8,9,10月は欠損しているものと思われる
期間によって、取り扱いを変える必要がありそう
- 下記期間でトレンドの変化が見られる
- 2016年1月〜7月
- 2016年8月〜10月
- 2016年11月〜12月
- 2017年1月〜4月
9.ホットペッパーグルメの予約データを結合
- こちらもキャンセル数はこのデータから把握することができない
# id横断データを読み込み store_id_df = pd.read_csv('Data/csv/store_id_relation.csv')
# 作成したair_dfのstore_idに、Airリザーブのstore_idを結合 air_df = pd.merge(air_df,store_id_df,on=['air_store_id'],how='left') air_df.tail(3)
| air_store_id | visit_date | visitors | reserve_visitors | hpg_store_id | |
|---|---|---|---|---|---|
| 252105 | air_24e8414b9b07decb | 2017-04-20 | 7 | NaN | NaN |
| 252106 | air_24e8414b9b07decb | 2017-04-21 | 8 | NaN | NaN |
| 252107 | air_24e8414b9b07decb | 2017-04-22 | 5 | NaN | NaN |
# 予約データを日次に加工 hpg_reserve_df = pd.read_csv('Data/csv/hpg_reserve.csv') hpg_reserve_df['visit_datetime'] = hpg_reserve_df['visit_datetime'].str[:10] hpg_reserve_df = hpg_reserve_df.rename(columns={'visit_datetime': 'visit_date'}).drop('reserve_datetime',axis=1) hpg_reserve_df = hpg_reserve_df.groupby(['hpg_store_id','visit_date'])['reserve_visitors'].sum().reset_index() hpg_reserve_df.tail(3)
| hpg_store_id | visit_date | reserve_visitors | |
|---|---|---|---|
| 1355050 | hpg_fffc097dce87af3e | 2017-03-27 | 5 |
| 1355051 | hpg_fffc097dce87af3e | 2017-04-21 | 3 |
| 1355052 | hpg_fffc097dce87af3e | 2017-04-23 | 8 |
# ホットペッパーグルメの予約データを結合 air_hpg_df = pd.merge(air_df,hpg_reserve_df,on=['hpg_store_id','visit_date'],how='left') air_hpg_df.tail(3)
| air_store_id | visit_date | visitors | reserve_visitors_x | hpg_store_id | reserve_visitors_y | |
|---|---|---|---|---|---|---|
| 252105 | air_24e8414b9b07decb | 2017-04-20 | 7 | NaN | NaN | NaN |
| 252106 | air_24e8414b9b07decb | 2017-04-21 | 8 | NaN | NaN | NaN |
| 252107 | air_24e8414b9b07decb | 2017-04-22 | 5 | NaN | NaN | NaN |
# Airリザーブとホットペッパーグルメの予約データを合算して、予約率を算出 air_hpg_df = DataFrame(air_hpg_df, columns=['air_store_id','hpg_store_id','visit_date','visitors','reserve_visitors','reserve_visitors_x','reserve_visitors_y']) air_hpg_df['reserve_visitors'] = air_hpg_df['reserve_visitors_x'].add(air_hpg_df['reserve_visitors_y'],fill_value=0) air_hpg_df = air_hpg_df.rename(columns={'reserve_visitors_x': 'reserve_visitors_air', 'reserve_visitors_y': 'reserve_visitors_hpg'}) air_hpg_df.tail(3)
| air_store_id | hpg_store_id | visit_date | visitors | reserve_visitors | reserve_visitors_air | reserve_visitors_hpg | |
|---|---|---|---|---|---|---|---|
| 252105 | air_24e8414b9b07decb | NaN | 2017-04-20 | 7 | NaN | NaN | NaN |
| 252106 | air_24e8414b9b07decb | NaN | 2017-04-21 | 8 | NaN | NaN | NaN |
| 252107 | air_24e8414b9b07decb | NaN | 2017-04-22 | 5 | NaN | NaN | NaN |
9–1.月次の訪問予定者数、訪問者数、予約訪問者率(訪問予定者数 / 訪問者数)
# データを月次に加工 air_hpg_monthly = air_hpg_df.loc[:,['visit_date','visitors','reserve_visitors','reserve_visitors_air','reserve_visitors_hpg']] air_hpg_monthly['visit_date'] = air_hpg_monthly.visit_date.str[:7] air_hpg_monthly = air_hpg_monthly.rename(columns={'visit_date': 'visit_month'}) air_hpg_monthly = air_hpg_monthly.groupby(['visit_month'])['visitors','reserve_visitors','reserve_visitors_air','reserve_visitors_hpg'].sum().reset_index() air_hpg_monthly['reserve_rate'] = air_hpg_monthly['reserve_visitors'] / air_hpg_monthly['visitors'] * 100 air_hpg_monthly.tail(3)
| visit_month | visitors | reserve_visitors | reserve_visitors_air | reserve_visitors_hpg | reserve_rate | |
|---|---|---|---|---|---|---|
| 13 | 2017-02 | 401462 | 55158.0 | 47963.0 | 7195.0 | 13.739283 |
| 14 | 2017-03 | 495487 | 72358.0 | 61065.0 | 11293.0 | 14.603410 |
| 15 | 2017-04 | 338236 | 43843.0 | 37493.0 | 6350.0 | 12.962251 |
air_hpg_monthly.describe(include='all')
| visit_month | visitors | reserve_visitors | reserve_visitors_air | reserve_visitors_hpg | reserve_rate | |
|---|---|---|---|---|---|---|
| count | 16 | 16.00000 | 16.000000 | 16.000000 | 16.000000 | 16.000000 |
| unique | 16 | NaN | NaN | NaN | NaN | NaN |
| top | 2017-01 | NaN | NaN | NaN | NaN | NaN |
| freq | 1 | NaN | NaN | NaN | NaN | NaN |
| mean | NaN | 330478.31250 | 29881.437500 | 24119.750000 | 5761.687500 | 8.644849 |
| std | NaN | 131525.06374 | 27187.080937 | 23720.900285 | 4189.623543 | 5.328091 |
| min | NaN | 152924.00000 | 5569.000000 | 2.000000 | 1418.000000 | 1.363948 |
| 25% | NaN | 181608.50000 | 10555.750000 | 6841.750000 | 2355.750000 | 3.665765 |
| 50% | NaN | 394155.00000 | 14780.000000 | 12612.000000 | 5829.000000 | 8.625267 |
| 75% | NaN | 420050.50000 | 48613.750000 | 42463.000000 | 6528.000000 | 13.046896 |
| max | NaN | 497617.00000 | 93584.000000 | 75556.000000 | 18028.000000 | 18.806431 |
# 棒グラフと折れ線グラフでプロット height1 = air_hpg_monthly.reserve_visitors_air.as_matrix() height2 = air_hpg_monthly.reserve_visitors_hpg.as_matrix() height3 = air_hpg_monthly.visitors.as_matrix() line_height = air_hpg_monthly.reserve_rate.as_matrix() w1 = 0.4 w2 = w1 / 2 left1 = np.arange(len(height1)) left2 = np.arange(len(height3)) fig, ax1 = plt.subplots(figsize=(14, 8)) p1 = ax1.bar(left1, height1, align='center', width=w1, tick_label=air_hpg_monthly.visit_month, color='deepskyblue') p2 = plt.bar(left1, height2, align="center", width=w1, bottom=height1, color='pink') p3 = ax1.bar(left2 + w1, height3, align='center', width=w1, tick_label=air_hpg_monthly.visit_month, color='navy') ax1.set_ylabel('Num of people') ax2 = ax1.twinx() p4 = ax2.plot(left1 + w2, line_height, color="red") ax2.set_ylabel('Reserve Rate') ax2.set_ylim(0, np.nanmax(line_height)*1.75) plt.legend((p1[0], p2[0], p3[0], p4[0]), ("air_reserve", "hpg_reserve", "visit", "reserve_rate"), loc='upper right', bbox_to_anchor=(0.7, 0.5, 0.5, 0.5))
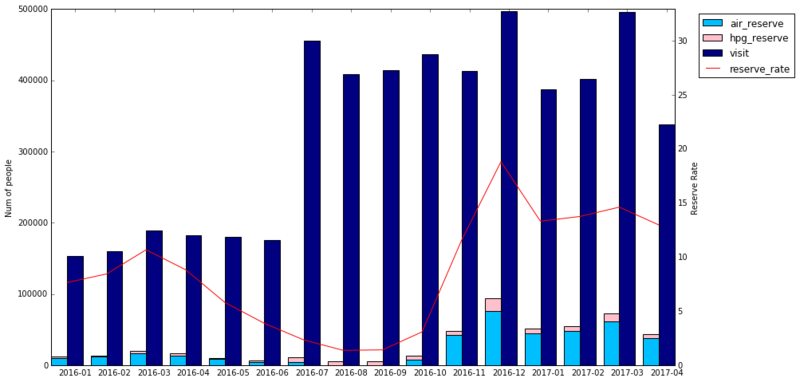
9–2.日次の訪問予定者数、訪問者数、予約訪問者率(訪問予定者数 / 訪問者数)
# 訪問データを日次で集計 air_hpg_df_daily = air_hpg_df.copy() air_hpg_df_daily['visit_date'] = air_hpg_df_daily.visit_date.map(lambda x: datetime.strptime(x,'%Y-%m-%d')) air_hpg_df_daily = air_hpg_df_daily.drop('air_store_id',axis=1) air_hpg_df_daily = air_hpg_df_daily.groupby(['visit_date'])['reserve_visitors','visitors'].sum().reset_index() air_hpg_df_daily.tail(3)
| visit_date | reserve_visitors | visitors | |
|---|---|---|---|
| 475 | 2017-04-20 | 1650.0 | 13990 |
| 476 | 2017-04-21 | 4262.0 | 19624 |
| 477 | 2017-04-22 | 3427.0 | 21245 |
# reserve_rate を追加して予約率を算出 air_hpg_df_daily['reserve_rate'] = air_hpg_df_daily['reserve_visitors'] / air_hpg_df_daily['visitors'] * 100 air_hpg_df_daily[air_hpg_df_daily['reserve_rate'] > 0].head(3)
| visit_date | reserve_visitors | visitors | reserve_rate | |
|---|---|---|---|---|
| 0 | 2016-01-01 | 21.0 | 1033 | 2.032914 |
| 1 | 2016-01-02 | 139.0 | 1764 | 7.879819 |
| 2 | 2016-01-03 | 75.0 | 2368 | 3.167230 |
air_hpg_df_daily.describe(include='all')
| visit_date | reserve_visitors | visitors | reserve_rate | |
|---|---|---|---|---|
| count | 478 | 478.000000 | 478.000000 | 478.000000 |
| unique | 478 | NaN | NaN | NaN |
| top | 2016-09-08 00:00:00 | NaN | NaN | NaN |
| freq | 1 | NaN | NaN | NaN |
| first | 2016-01-01 00:00:00 | NaN | NaN | NaN |
| last | 2017-04-22 00:00:00 | NaN | NaN | NaN |
| mean | NaN | 1000.215481 | 11062.035565 | 8.175872 |
| std | NaN | 1111.148722 | 5079.505034 | 5.752625 |
| min | NaN | 21.000000 | 1033.000000 | 0.477484 |
| 25% | NaN | 238.250000 | 5894.500000 | 2.828093 |
| 50% | NaN | 513.500000 | 11429.500000 | 8.044074 |
| 75% | NaN | 1344.750000 | 14286.000000 | 11.572778 |
| max | NaN | 6222.000000 | 23982.000000 | 29.372503 |
# 折れ線グラフで描画 line_height1 = air_hpg_df_daily.reserve_visitors.as_matrix() line_height2 = air_hpg_df_daily.visitors.as_matrix() line_height3 = air_hpg_df_daily.reserve_rate.as_matrix() left = air_hpg_df_daily.visit_date fig, ax1 = plt.subplots(figsize=(18, 10)) p1 = plt.plot(left, line_height1, color="deepskyblue") p2 = plt.plot(left, line_height2, color="navy") ax1.set_ylabel('Num of people') ax2 = ax1.twinx() p3 = ax2.plot(left, line_height3, color="red") ax2.set_ylabel('Reserve Rate') ax2.set_ylim(0, 50) plt.legend((p1[0], p2[0], p3[0]), ("reserve", "visit", "reserve_rate"), loc='upper right', bbox_to_anchor=(0.7, 0.5, 0.5, 0.5)) plt.title("daily_visitors") plt.xlabel("visit_date") plt.grid(True)

9–3.気づき
ホットペッパーの訪問データを足すことによる、発見したトレンドへの影響はほとんどない
10.レストラン情報を結合
10–1.Airリザーブのレストラン情報を結合
# Airリザーブのレストラン情報を読み込み air_store_df = pd.read_csv('Data/csv/air_store_info.csv') air_store_df.head(3)
| air_store_id | air_genre_name | air_area_name | latitude | longitude | |
|---|---|---|---|---|---|
| 0 | air_0f0cdeee6c9bf3d7 | Italian/French | Hyōgo-ken Kōbe-shi Kumoidōri | 34.695124 | 135.197852 |
| 1 | air_7cc17a324ae5c7dc | Italian/French | Hyōgo-ken Kōbe-shi Kumoidōri | 34.695124 | 135.197852 |
| 2 | air_fee8dcf4d619598e | Italian/French | Hyōgo-ken Kōbe-shi Kumoidōri | 34.695124 | 135.197852 |
# Airリザーブのレストラン情報を結合 airi_hpg_df = pd.merge(air_hpg_df,air_store_df,on=['air_store_id'],how='left') airi_hpg_df = airi_hpg_df.rename(columns={'latitude': 'latitude_air', 'longitude': 'longitude_air'}) airi_hpg_df.tail(3)
| air_store_id | hpg_store_id | visit_date | visitors | reserve_visitors | reserve_visitors_air | reserve_visitors_hpg | air_genre_name | air_area_name | latitude_air | longitude_air | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 252105 | air_24e8414b9b07decb | NaN | 2017-04-20 | 7 | NaN | NaN | NaN | Other | Tōkyō-to Shibuya-ku Higashi | 35.653217 | 139.711036 |
| 252106 | air_24e8414b9b07decb | NaN | 2017-04-21 | 8 | NaN | NaN | NaN | Other | Tōkyō-to Shibuya-ku Higashi | 35.653217 | 139.711036 |
| 252107 | air_24e8414b9b07decb | NaN | 2017-04-22 | 5 | NaN | NaN | NaN | Other | Tōkyō-to Shibuya-ku Higashi | 35.653217 | 139.711036 |
10–2.ホットペッパーグルメのレストラン情報を結合
# ホットペッパーグルメのレストラン情報を読み込み hpg_store_df = pd.read_csv('Data/csv/hpg_store_info.csv') hpg_store_df.head(3)
| hpg_store_id | hpg_genre_name | hpg_area_name | latitude | longitude | |
|---|---|---|---|---|---|
| 0 | hpg_6622b62385aec8bf | Japanese style | Tōkyō-to Setagaya-ku Taishidō | 35.643675 | 139.668221 |
| 1 | hpg_e9e068dd49c5fa00 | Japanese style | Tōkyō-to Setagaya-ku Taishidō | 35.643675 | 139.668221 |
| 2 | hpg_2976f7acb4b3a3bc | Japanese style | Tōkyō-to Setagaya-ku Taishidō | 35.643675 | 139.668221 |
# Aホットペッパーグルメのレストラン情報を結合 airi_hpgi_df = pd.merge(airi_hpg_df,hpg_store_df,on=['hpg_store_id'],how='left') airi_hpgi_df = airi_hpgi_df.rename(columns={'latitude': 'latitude_hpg', 'longitude': 'longitude_hpg'}) airi_hpgi_df.tail(3)
| air_store_id | hpg_store_id | visit_date | visitors | reserve_visitors | reserve_visitors_air | reserve_visitors_hpg | air_genre_name | air_area_name | latitude_air | longitude_air | hpg_genre_name | hpg_area_name | latitude_hpg | longitude_hpg | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 252105 | air_24e8414b9b07decb | NaN | 2017-04-20 | 7 | NaN | NaN | NaN | Other | Tōkyō-to Shibuya-ku Higashi | 35.653217 | 139.711036 | NaN | NaN | NaN | NaN |
| 252106 | air_24e8414b9b07decb | NaN | 2017-04-21 | 8 | NaN | NaN | NaN | Other | Tōkyō-to Shibuya-ku Higashi | 35.653217 | 139.711036 | NaN | NaN | NaN | NaN |
| 252107 | air_24e8414b9b07decb | NaN | 2017-04-22 | 5 | NaN | NaN | NaN | Other | Tōkyō-to Shibuya-ku Higashi | 35.653217 | 139.711036 | NaN | NaN | NaN | NaN |
airi_hpgi_df.describe(include='all')
| air_store_id | hpg_store_id | visit_date | visitors | reserve_visitors | reserve_visitors_air | reserve_visitors_hpg | air_genre_name | air_area_name | latitude_air | longitude_air | hpg_genre_name | hpg_area_name | latitude_hpg | longitude_hpg | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 252108 | 46019 | 252108 | 252108.000000 | 35698.000000 | 28064.000000 | 13550.000000 | 252108 | 252108 | 252108.000000 | 252108.000000 | 20098 | 20098 | 20098.000000 | 20098.000000 |
| unique | 829 | 150 | 478 | NaN | NaN | NaN | NaN | 14 | 103 | NaN | NaN | 16 | 33 | NaN | NaN |
| top | air_5c817ef28f236bdf | hpg_f83413cde79ac5e7 | 2017-03-17 | NaN | NaN | NaN | NaN | Izakaya | Fukuoka-ken Fukuoka-shi Daimyō | NaN | NaN | Japanese style | Tōkyō-to Shibuya-ku None | NaN | NaN |
| freq | 477 | 473 | 799 | NaN | NaN | NaN | NaN | 62052 | 19775 | NaN | NaN | 6770 | 1709 | NaN | NaN |
| mean | NaN | NaN | NaN | 20.973761 | 13.392991 | 13.751283 | 6.803469 | NaN | NaN | 35.613121 | 137.357865 | NaN | NaN | 36.316416 | 137.161974 |
| std | NaN | NaN | NaN | 16.757007 | 17.141707 | 17.284799 | 7.686077 | NaN | NaN | 2.044473 | 3.671577 | NaN | NaN | 3.009303 | 3.881765 |
| min | NaN | NaN | NaN | 1.000000 | 1.000000 | 1.000000 | 1.000000 | NaN | NaN | 33.211967 | 130.195555 | NaN | NaN | 33.556881 | 130.392801 |
| 25% | NaN | NaN | NaN | 9.000000 | 4.000000 | 5.000000 | 2.000000 | NaN | NaN | 34.692337 | 135.341564 | NaN | NaN | 34.669514 | 134.847642 |
| 50% | NaN | NaN | NaN | 17.000000 | 9.000000 | 10.000000 | 4.000000 | NaN | NaN | 35.658068 | 139.670038 | NaN | NaN | 35.659214 | 139.060024 |
| 75% | NaN | NaN | NaN | 29.000000 | 18.000000 | 18.000000 | 8.000000 | NaN | NaN | 35.694003 | 139.751599 | NaN | NaN | 35.711353 | 139.737998 |
| max | NaN | NaN | NaN | 877.000000 | 1633.000000 | 1633.000000 | 157.000000 | NaN | NaN | 44.020632 | 144.273398 | NaN | NaN | 43.768033 | 142.359664 |
10–3.都道府県ごとの訪問者数
# Airのエリアを採用し、都道府県ごとの訪問者数を集計 airi_hpgi_df_area = airi_hpgi_df.copy() airi_hpgi_df_area['air_area_name'] = airi_hpgi_df_area.air_area_name.map(lambda x: ' '.join(x.split(' ')[:1]).translate(str.maketrans('Ōōū', 'Oou'))) airi_hpgi_df_area['visit_date'] = airi_hpgi_df_area.visit_date.map(lambda x: datetime.strptime(x,'%Y-%m-%d')) airi_hpgi_df_area = airi_hpgi_df_area.groupby(['visit_date','air_area_name'])['visitors'].sum().reset_index() airi_hpgi_df_area.head(3)
| visit_date | air_area_name | visitors | |
|---|---|---|---|
| 0 | 2016-01-01 | Fukuoka-ken | 272 |
| 1 | 2016-01-01 | Hiroshima-ken | 42 |
| 2 | 2016-01-01 | Hokkaido | 20 |
# 折れ線グラフで描画 line_height1 = airi_hpgi_df_area[airi_hpgi_df_area['air_area_name'] == 'Tokyo-to'].visitors.as_matrix() line_height2 = airi_hpgi_df_area[airi_hpgi_df_area['air_area_name'] == 'Osaka-fu'].visitors.as_matrix() line_height3 = airi_hpgi_df_area[airi_hpgi_df_area['air_area_name'] == 'Fukuoka-ken'].visitors.as_matrix() left = airi_hpgi_df_area.visit_date.drop_duplicates() fig, (ax1,ax2,ax3) = plt.subplots(nrows=3, figsize=(18,10)) ax1.plot(left, line_height1, color="orange") ax1.set_title('Tokyo') ax1.grid(True) ax2.plot(left, line_height2, color="black") ax2.set_title('Osaka') ax2.set_ylabel('Number_of_people') ax2.grid(True) ax3.plot(left, line_height3, color="yellow") ax3.set_title('Fukuoka') ax3.set_xlabel('visit_date') ax3.grid(True)
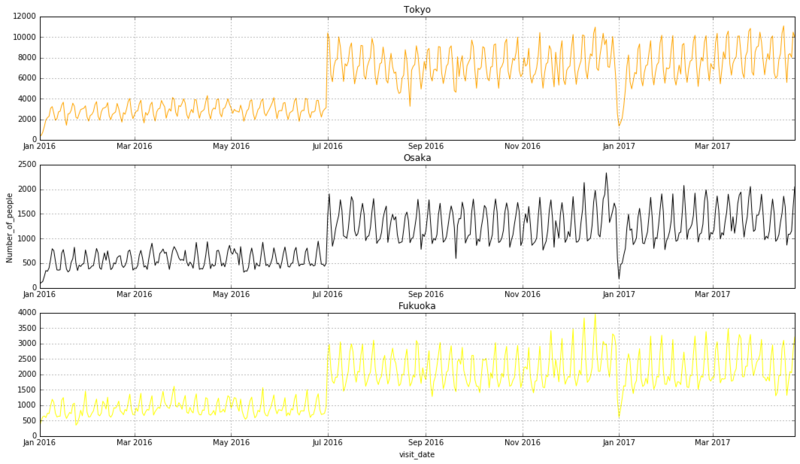
10–4.ジャンルごとの訪問者数
# Airのジャンルを採用し、都道府県ごとの訪問者数を集計 airi_hpgi_df_genre = airi_hpgi_df.copy() airi_hpgi_df_genre['air_area_name'] = airi_hpgi_df_genre.air_area_name.map(lambda x: ' '.join(x.split(' ')[:1]).translate(str.maketrans('Ōōū', 'Oou'))) airi_hpgi_df_genre['visit_date'] = airi_hpgi_df_genre.visit_date.map(lambda x: datetime.strptime(x,'%Y-%m-%d')) airi_hpgi_df_genre = airi_hpgi_df_genre.groupby(['visit_date','air_genre_name'])['visitors'].sum().reset_index() airi_hpgi_df_genre.head(3)
| visit_date | air_genre_name | visitors | |
|---|---|---|---|
| 0 | 2016-01-01 | Bar/Cocktail | 136 |
| 1 | 2016-01-01 | Cafe/Sweets | 266 |
| 2 | 2016-01-01 | Creative cuisine | 7 |
# 折れ線グラフで描画 line_height1 = airi_hpgi_df_genre[airi_hpgi_df_genre['air_genre_name'] == 'Izakaya'].visitors.as_matrix() line_height2 = airi_hpgi_df_genre[airi_hpgi_df_genre['air_genre_name'] == 'Cafe/Sweets'].visitors.as_matrix() line_height3 = airi_hpgi_df_genre[airi_hpgi_df_genre['air_genre_name'] == 'Dining bar'].visitors.as_matrix() left = airi_hpgi_df_genre.visit_date.drop_duplicates() fig, (ax1,ax2,ax3) = plt.subplots(nrows=3, figsize=(18,10)) ax1.plot(left, line_height1, color="c") ax1.set_title('Izakaya') ax1.grid(True) ax2.plot(left, line_height2, color="r") ax2.set_title('Cafe/Sweets') ax2.set_ylabel('Number_of_people') ax2.grid(True) ax3.plot(left, line_height3, color="b") ax3.set_title('Dining bar') ax3.set_xlabel('visit_date') ax3.grid(True)
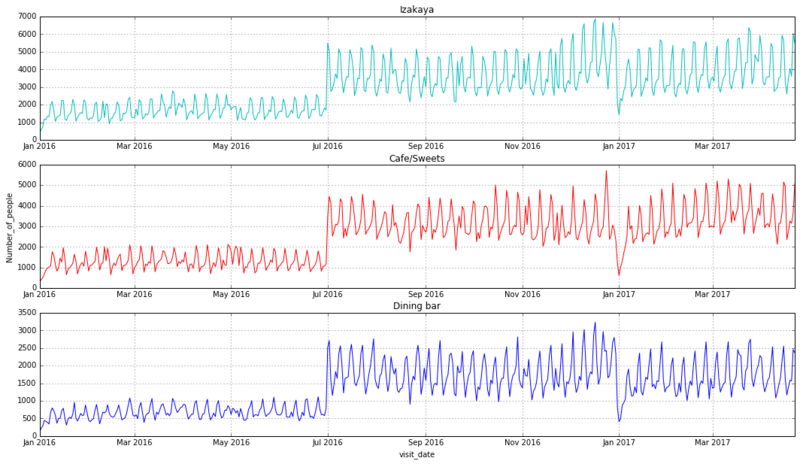
10–5.気づき
エリアやジャンルによって、トレンドに目立った違いは見られない
- 機械学習で見えない特徴を掴もう
11.カレンダー情報を結合
# カレンダーを読み込み calendar_df = pd.read_csv('Data/csv/date_info.csv') calendar_df.head()
| calendar_date | day_of_week | holiday_flg | |
|---|---|---|---|
| 0 | 2016-01-01 | Friday | 1 |
| 1 | 2016-01-02 | Saturday | 1 |
| 2 | 2016-01-03 | Sunday | 1 |
| 3 | 2016-01-04 | Monday | 0 |
| 4 | 2016-01-05 | Tuesday | 0 |
# カレンダー情報を結合 calendar_df = calendar_df.rename(columns={'calendar_date': 'visit_date'}) comp_df = pd.merge(airi_hpgi_df,calendar_df,on=['visit_date'],how='left') comp_df.head(3)
| air_store_id | hpg_store_id | visit_date | visitors | reserve_visitors | reserve_visitors_air | reserve_visitors_hpg | air_genre_name | air_area_name | latitude_air | longitude_air | hpg_genre_name | hpg_area_name | latitude_hpg | longitude_hpg | day_of_week | holiday_flg | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | air_ba937bf13d40fb24 | NaN | 2016-01-13 | 25 | NaN | NaN | NaN | Dining bar | Tōkyō-to Minato-ku Shibakōen | 35.658068 | 139.751599 | NaN | NaN | NaN | NaN | Wednesday | 0 |
| 1 | air_ba937bf13d40fb24 | NaN | 2016-01-14 | 32 | NaN | NaN | NaN | Dining bar | Tōkyō-to Minato-ku Shibakōen | 35.658068 | 139.751599 | NaN | NaN | NaN | NaN | Thursday | 0 |
| 2 | air_ba937bf13d40fb24 | NaN | 2016-01-15 | 29 | NaN | NaN | NaN | Dining bar | Tōkyō-to Minato-ku Shibakōen | 35.658068 | 139.751599 | NaN | NaN | NaN | NaN | Friday | 0 |
Kaggleに挑戦する - 与えられたデータの確認1
かねてから挑戦して見たかったKaggleに挑戦する(つもりだった...)
そのコンペは終了してしまったため、Submitはできないのだが、せっかく着手していたのでやりきりたい。
対象のコンペは、Recruit Restaurant Visitor Forecasting。
飲食店の来客数を予想する。
Recruit Restaurant Visitor Forecasting | Kaggle
これから数回に分けて、基礎分析から機械学習を用いた予測まで、一連の作業を進めていく。
最新のソースはGitHubで公開、随時更新していく。
今回は与えられたデータの確認1回目。
与えられたcsvデータどうしを結合せずに分析していきます。
0.sample_submission.csv [Submitサンプル]
- store_idに、アンダースコア、訪問日を付与する必要がある
- 2017-04-23〜2017-05-31が予測対象期間
- visitorsに予測値を出力する
import numpy as np import pandas as pd from pandas import DataFrame from datetime import datetime, timedelta import seaborn as sns import matplotlib.pyplot as plt %matplotlib inline
# .csvをDataFrame化 sample = pd.read_csv('Data/csv/sample_submission.csv') sample.head(3)
| id | visitors | |
|---|---|---|
| 0 | air_00a91d42b08b08d9_2017-04-23 | 0 |
| 1 | air_00a91d42b08b08d9_2017-04-24 | 0 |
| 2 | air_00a91d42b08b08d9_2017-04-25 | 0 |
# 他のデータセットと形式を合わせておく sample_edit = sample.copy() sample_edit['air_store_id'] = sample_edit.id.map(lambda x: '_'.join(x.split('_')[:-1])) sample_edit['calendar_date'] = sample_edit.id.map(lambda x: x.split('_')[2]) sample_edit['calendar_date'] = sample_edit.calendar_date.map(lambda x: datetime.strptime(x,'%Y-%m-%d')) sample_edit.drop('id',axis=1) sample_edit = sample_edit.loc[:,['air_store_id','calendar_date','visitors']] sample_edit.head(3)
| air_store_id | calendar_date | visitors | |
|---|---|---|---|
| 0 | air_00a91d42b08b08d9 | 2017-04-23 | 0 |
| 1 | air_00a91d42b08b08d9 | 2017-04-24 | 0 |
| 2 | air_00a91d42b08b08d9 | 2017-04-25 | 0 |
# データ型を確認
sample_edit.dtypes
air_store_id object
calendar_date datetime64[ns]
visitors int64
dtype: object
# 統計量を確認 sample_edit.describe(include='all')
| air_store_id | calendar_date | visitors | |
|---|---|---|---|
| count | 32019 | 32019 | 32019.0 |
| unique | 821 | 39 | NaN |
| top | air_b88192b35ac03c24 | 2017-05-26 00:00:00 | NaN |
| freq | 39 | 821 | NaN |
| first | NaN | 2017-04-23 00:00:00 | NaN |
| last | NaN | 2017-05-31 00:00:00 | NaN |
| mean | NaN | NaN | 0.0 |
| std | NaN | NaN | 0.0 |
| min | NaN | NaN | 0.0 |
| 25% | NaN | NaN | 0.0 |
| 50% | NaN | NaN | 0.0 |
| 75% | NaN | NaN | 0.0 |
| max | NaN | NaN | 0.0 |
1.air_reserve.csv [Airリザーブの予約データ]
- 92,378レコード
- 314 /829店舗分の予約データ
- 訪問予定は、2016-01-01 19:00:00 〜 2017-05-31 21:00:00
- 予約時刻は、2016-01-01 01:00:00 〜 2017-04-22 23:00:00
# .csvをDataFrame化 df1 = pd.read_csv('Data/csv/air_reserve.csv') df1.head(3)
| air_store_id | visit_datetime | reserve_datetime | reserve_visitors | |
|---|---|---|---|---|
| 0 | air_877f79706adbfb06 | 2016-01-01 19:00:00 | 2016-01-01 16:00:00 | 1 |
| 1 | air_db4b38ebe7a7ceff | 2016-01-01 19:00:00 | 2016-01-01 19:00:00 | 3 |
| 2 | air_db4b38ebe7a7ceff | 2016-01-01 19:00:00 | 2016-01-01 19:00:00 | 6 |
# データ型を確認
df1.dtypes
air_store_id object
visit_datetime object
reserve_datetime object
reserve_visitors int64
dtype: object
# データ型を修正 df1['visit_datetime'] = df1.visit_datetime.map(lambda x: datetime.strptime(x,'%Y-%m-%d %H:%M:%S')) df1['reserve_datetime'] = df1.reserve_datetime.map(lambda x: datetime.strptime(x,'%Y-%m-%d %H:%M:%S')) df1.dtypes
air_store_id object
visit_datetime datetime64[ns]
reserve_datetime datetime64[ns]
reserve_visitors int64
dtype: object
# 統計量を確認 df1.describe(include='all')
| air_store_id | visit_datetime | reserve_datetime | reserve_visitors | |
|---|---|---|---|---|
| count | 92378 | 92378 | 92378 | 92378.000000 |
| unique | 314 | 4975 | 7513 | NaN |
| top | air_8093d0b565e9dbdf | 2016-12-24 19:00:00 | 2016-11-24 18:00:00 | NaN |
| freq | 2263 | 255 | 106 | NaN |
| first | NaN | 2016-01-01 19:00:00 | 2016-01-01 01:00:00 | NaN |
| last | NaN | 2017-05-31 21:00:00 | 2017-04-22 23:00:00 | NaN |
| mean | NaN | NaN | NaN | 4.481749 |
| std | NaN | NaN | NaN | 4.919669 |
| min | NaN | NaN | NaN | 1.000000 |
| 25% | NaN | NaN | NaN | 2.000000 |
| 50% | NaN | NaN | NaN | 3.000000 |
| 75% | NaN | NaN | NaN | 5.000000 |
| max | NaN | NaN | NaN | 100.000000 |
1−1.月間予約数
# 予約数を月次で集計 df1_monthly = df1.copy() df1_monthly['reserve_datetime'] = df1_monthly.reserve_datetime.map(lambda x: x.strftime('%Y-%m')) drop_col = ['air_store_id','visit_datetime'] df1_monthly = df1_monthly.rename(columns={'reserve_datetime': 'reserve_month'}).drop(drop_col,axis=1) df1_monthly = df1_monthly.groupby(['reserve_month']).count().reset_index().rename(columns={'reserve_visitors':'reserve'}) df1_monthly.head(3)
| reserve_month | reserve | |
|---|---|---|
| 0 | 2016-01 | 2936 |
| 1 | 2016-02 | 2999 |
| 2 | 2016-03 | 3643 |
# 棒グラフで描画 plt.figure(figsize=(14, 8)) plt.bar(np.arange(1,17), df1_monthly.reserve.as_matrix(), tick_label=df1_monthly.reserve_month, align="center", color='deepskyblue') plt.title("Monthly_air_reserve") plt.xticks(rotation = 30) plt.xlabel("month") plt.ylabel("reserve") plt.grid(True)
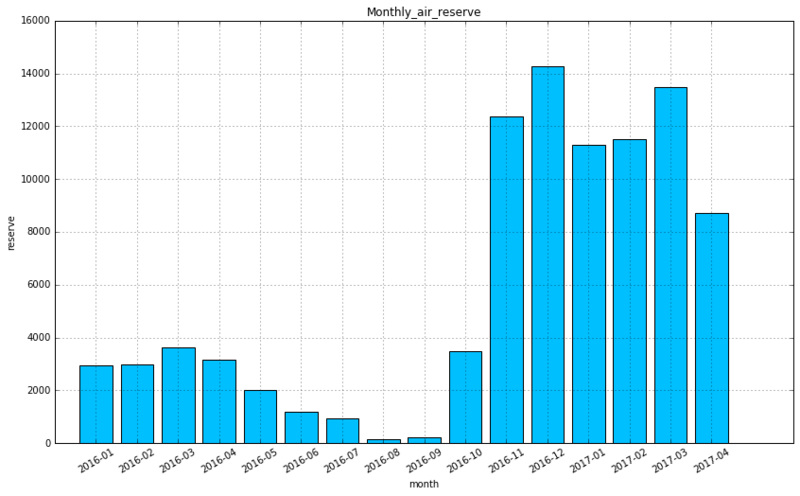
1−2.月別訪問予定者数
# 訪問予定者数を月次で集計 df1_monthly = df1.copy() df1_monthly['visit_datetime'] = df1_monthly.visit_datetime.map(lambda x: x.strftime('%Y-%m')) drop_col = ['air_store_id','reserve_datetime'] df1_monthly = df1_monthly.rename(columns={'visit_datetime': 'visit_month'}).drop(drop_col,axis=1) df1_monthly = df1_monthly.groupby(['visit_month'])['reserve_visitors'].sum().reset_index() df1_monthly.head(3)
| visit_month | reserve_visitors | |
|---|---|---|
| 0 | 2016-01 | 10335 |
| 1 | 2016-02 | 11579 |
| 2 | 2016-03 | 17071 |
# 棒グラフで描画 plt.figure(figsize=(14, 8)) plt.bar(np.arange(1,18), df1_monthly.reserve_visitors.as_matrix(), tick_label=df1_monthly.visit_month, align="center", color='deepskyblue') plt.title("Monthly_air_reserve_visitors") plt.xticks(rotation = 30) plt.xlabel("month") plt.ylabel("reserve_visitors") plt.grid(True)
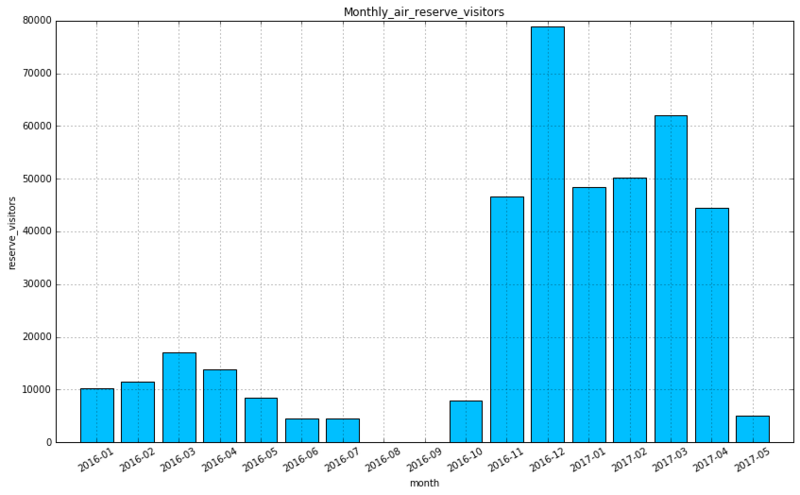
1−3.予約日から訪問予定日までの日数
# 予約日から訪問予定日までの日数を追加 df1_monthly_diff = df1.copy() df1_monthly_diff['rsrv_2_vst'] = df1_monthly_diff.visit_datetime - df1_monthly_diff.reserve_datetime df1_monthly_diff['rsrv_2_vst'] = df1_monthly_diff.rsrv_2_vst.map(lambda x: x.days) df1_monthly_diff['reserve_datetime'] = df1_monthly_diff.reserve_datetime.map(lambda x: x.strftime('%Y-%m')) df1_monthly_diff = df1_monthly_diff.rename(columns={'reserve_datetime': 'reserve_month'}) df1_monthly_diff.tail(3)
| air_store_id | visit_datetime | reserve_month | reserve_visitors | rsrv_2_vst | |
|---|---|---|---|---|---|
| 92375 | air_877f79706adbfb06 | 2017-05-31 20:00:00 | 2017-04 | 3 | 48 |
| 92376 | air_900d755ebd2f7bbd | 2017-05-31 20:00:00 | 2017-04 | 10 | 42 |
| 92377 | air_3cad29d1a23209d2 | 2017-05-31 21:00:00 | 2017-04 | 3 | 39 |
plt.figure(figsize=(14, 8)) sns.boxplot(x="reserve_month", y="rsrv_2_vst", data=df1_monthly_diff)
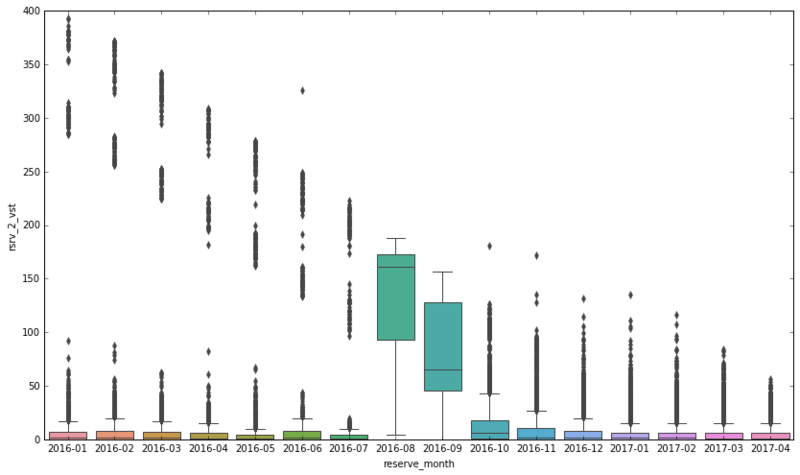
1−4.気づき
2016年9月以前の訪問者数がそれ以降に比べて少ない
- 2016年7月まで先行展開、2016年10月から本格展開の可能性がある
- データがサンプリングされている可能性がある
忘年会、納会シーズンの予約が多い一方、歓迎会シーズンはそれほどでもないように見える
- 休日祝日の日数による影響がある可能性がある
5月以降の訪問予定になっている予約データはおそらく、意図的に除外されている
- 1年前、10か月前から予約が可能な人気店がある
- 5月以降の訪問予定になっている予約データはおそらく、意図的に除外されている(除外されていないレコードも5,000弱存在はする)
2.air_visit_data.csv [Airリザーブの訪問データ]
- 252,108レコード
- 829店舗全ての履歴データがある
- 訪問日時は、2016-01-01 〜 2017-04-22
# .csvをDataFrame化 df3 = pd.read_csv('Data/csv/air_visit_data.csv') df3.head(3)
| air_store_id | visit_date | visitors | |
|---|---|---|---|
| 0 | air_ba937bf13d40fb24 | 2016-01-13 | 25 |
| 1 | air_ba937bf13d40fb24 | 2016-01-14 | 32 |
| 2 | air_ba937bf13d40fb24 | 2016-01-15 | 29 |
# データ型を確認
df3.dtypes
air_store_id object
visit_date object
visitors int64
dtype: object
# データ型を修正 df3['visit_date'] = df3.visit_date.map(lambda x: datetime.strptime(x,'%Y-%m-%d')) df3.dtypes
air_store_id object
visit_date datetime64[ns]
visitors int64
dtype: object
# 統計量を確認 df3.describe(include='all')
| air_store_id | visit_date | visitors | |
|---|---|---|---|
| count | 252108 | 252108 | 252108.000000 |
| unique | 829 | 478 | NaN |
| top | air_5c817ef28f236bdf | 2017-03-17 00:00:00 | NaN |
| freq | 477 | 799 | NaN |
| first | NaN | 2016-01-01 00:00:00 | NaN |
| last | NaN | 2017-04-22 00:00:00 | NaN |
| mean | NaN | NaN | 20.973761 |
| std | NaN | NaN | 16.757007 |
| min | NaN | NaN | 1.000000 |
| 25% | NaN | NaN | 9.000000 |
| 50% | NaN | NaN | 17.000000 |
| 75% | NaN | NaN | 29.000000 |
| max | NaN | NaN | 877.000000 |
2−1.月間訪問者数
# 訪問データを月次に加工 df3_monthly = df3.copy() df3_monthly['visit_date'] = df3_monthly.visit_date.map(lambda x: x.strftime('%Y-%m')) df3_monthly = df3_monthly.rename(columns={'visit_date': 'visit_month'}) df3_monthly = df3_monthly.groupby(['visit_month'])['visitors'].sum().reset_index() df3_monthly.head(3)
| visit_month | visitors | |
|---|---|---|
| 0 | 2016-01 | 152924 |
| 1 | 2016-02 | 159934 |
| 2 | 2016-03 | 189292 |
# 棒グラフで描画 plt.figure(figsize=(14, 8)) plt.bar(np.arange(1,17), df3_monthly.visitors.as_matrix(), tick_label=df3_monthly.visit_month, align="center", color='navy') plt.title("Monthly_air_visitors") plt.xticks(rotation = 30) plt.xlabel("month") plt.ylabel("visitors") plt.grid(True)
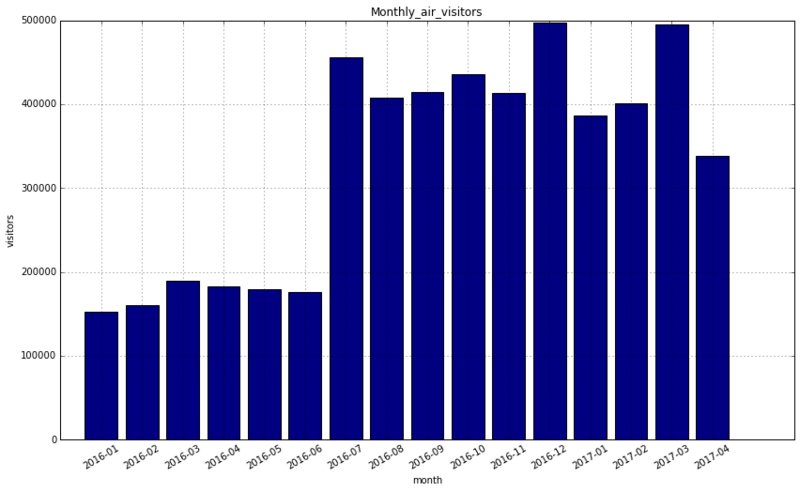
2−2.一日の訪問者数
# 訪問予定月を追加 df3_monthly_diff = df3.copy() df3_monthly_diff['visit_month'] = df3_monthly_diff.visit_date.map(lambda x: x.strftime('%Y-%m')) df3_monthly_diff.tail(3)
| air_store_id | visit_date | visitors | visit_month | |
|---|---|---|---|---|
| 252105 | air_24e8414b9b07decb | 2017-04-20 | 7 | 2017-04 |
| 252106 | air_24e8414b9b07decb | 2017-04-21 | 8 | 2017-04 |
| 252107 | air_24e8414b9b07decb | 2017-04-22 | 5 | 2017-04 |
plt.figure(figsize=(14, 8)) sns.boxplot(x="visit_month", y="visitors", data=df3_monthly_diff)
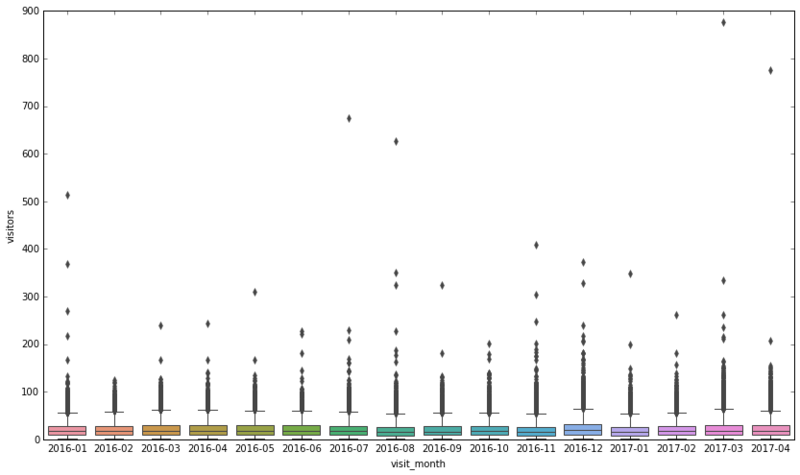
2−3.予約データと並べて予約率を見てみる
※予約と実訪問日をキーに結合した値ではないため、参考程度に
# 棒グラフと折れ線グラフで描画する height1 = df1_monthly.reserve_visitors.as_matrix() height2 = df3_monthly.visitors.as_matrix() line_height = (df1_monthly.reserve_visitors / df3_monthly.visitors * 100).as_matrix() w1 = 0.4 w2 = w1 / 2 left1 = np.arange(len(height1)) left2 = np.arange(len(height2)) fig, ax1 = plt.subplots(figsize=(14, 8)) p1 = ax1.bar(left1, height1, align='center', width=w1, tick_label=df1_monthly.visit_month, color='deepskyblue') p2 = ax1.bar(left2 + w1, height2, align='center', width=w1, tick_label=df3_monthly.visit_month, color='navy') ax1.set_ylabel('Num of people') ax2 = ax1.twinx() p3 = ax2.plot(left1 + w2, line_height, color="red") ax2.set_ylabel('Reserve Rate') ax2.set_ylim(0, np.nanmax(line_height)*1.75) plt.legend((p1[0], p2[0], p3[0]), ("reserve", "visit", "reserve_rate"), loc='upper right', bbox_to_anchor=(0.7, 0.5, 0.5, 0.5))
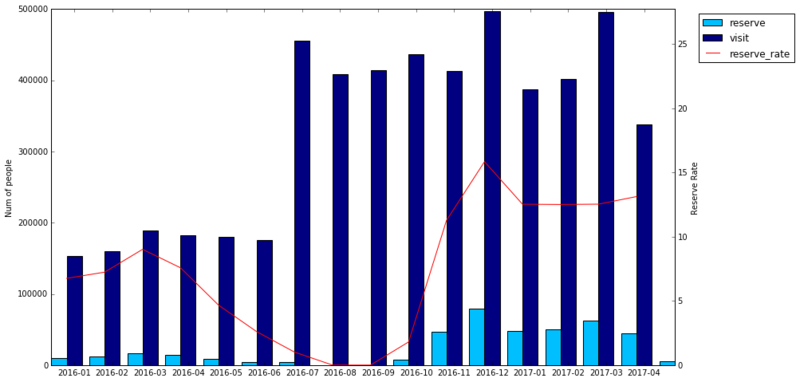
2–4.気づき
大口の予約が混ざっている
- 100名を超えるような大口の予約も混ざっている
予約データと訪問データで充実している期間が異なる
- 予約データは2016年11月以降、訪問データは2016年7月以降で充実している
- 2016年7月まで先行展開、2016年10月から本格展開の可能性は否定すべきか
- 予約機能と決済機能の展開時期が異なっていたと考えることもできる
3.air_store_info.csv [Airリザーブのレストラン情報]
- 829店舗
- 14ジャンル
- 103エリア
# .csvをDataFrame化 df2 = pd.read_csv('Data/csv/air_store_info.csv') df2.head(3)
| air_store_id | air_genre_name | air_area_name | latitude | longitude | |
|---|---|---|---|---|---|
| 0 | air_0f0cdeee6c9bf3d7 | Italian/French | Hyōgo-ken Kōbe-shi Kumoidōri | 34.695124 | 135.197852 |
| 1 | air_7cc17a324ae5c7dc | Italian/French | Hyōgo-ken Kōbe-shi Kumoidōri | 34.695124 | 135.197852 |
| 2 | air_fee8dcf4d619598e | Italian/French | Hyōgo-ken Kōbe-shi Kumoidōri | 34.695124 | 135.197852 |
# データ型を確認
df2.dtypes
air_store_id object
air_genre_name object
air_area_name object
latitude float64
longitude float64
dtype: object
# 統計量を確認 df2.describe(include='all')
| air_store_id | air_genre_name | air_area_name | latitude | longitude | |
|---|---|---|---|---|---|
| count | 829 | 829 | 829 | 829.000000 | 829.000000 |
| unique | 829 | 14 | 103 | NaN | NaN |
| top | air_eb5788dba285e725 | Izakaya | Fukuoka-ken Fukuoka-shi Daimyō | NaN | NaN |
| freq | 1 | 197 | 64 | NaN | NaN |
| mean | NaN | NaN | NaN | 35.647042 | 137.415311 |
| std | NaN | NaN | NaN | 2.084659 | 3.650971 |
| min | NaN | NaN | NaN | 33.211967 | 130.195555 |
| 25% | NaN | NaN | NaN | 34.695124 | 135.341564 |
| 50% | NaN | NaN | NaN | 35.658068 | 139.685474 |
| 75% | NaN | NaN | NaN | 35.694003 | 139.751599 |
| max | NaN | NaN | NaN | 44.020632 | 144.273398 |
3−1.ジャンルごとの店舗数
# ジャンルの内訳と頻度 df2.groupby('air_genre_name').size().sort_values(ascending=False).describe()
count 14.000000
mean 59.214286
std 66.013027
min 2.000000
25% 13.250000
50% 25.000000
75% 96.250000
max 197.000000
dtype: float64
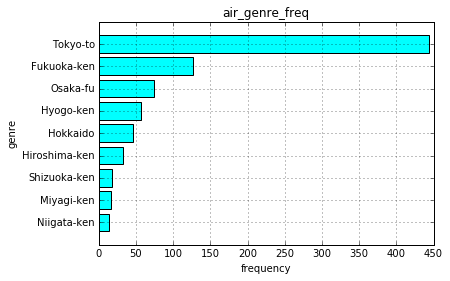
# 棒グラフで描画 df2_air_genre_name = df2.groupby('air_genre_name').size().sort_values() plt.barh(np.arange(1,15), df2_air_genre_name.values, tick_label=df2_air_genre_name.index, align="center", color='dodgerblue') plt.title("air_genre_freq") plt.xlabel("frequency") plt.ylabel("genre") plt.grid(True)
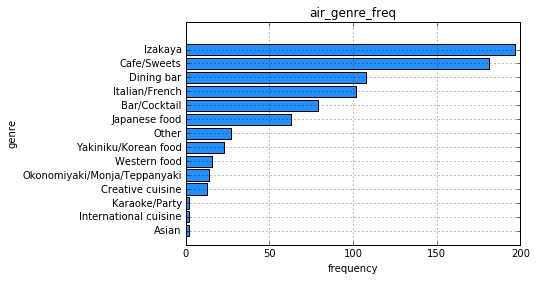
3−2.エリアごとの店舗数
# エリアの内訳と頻度 df2.groupby('air_area_name').size().sort_values(ascending=False).describe()
count 103.000000
mean 8.048544
std 11.332219
min 2.000000
25% 2.000000
50% 4.000000
75% 7.500000
max 64.000000
dtype: float64
3−2−1.市区町村ごとの店舗数
# エリアを市区町村レベルに変更、plot時の文字化け対策で置換 df2_city = df2.copy() df2_city['air_area_name'] = df2_city.air_area_name.map(lambda x: ' '.join(x.split(' ')[:2]).translate(str.maketrans('Ōōū', 'Oou'))) df2_city.head(3)
| air_store_id | air_genre_name | air_area_name | latitude | longitude | |
|---|---|---|---|---|---|
| 0 | air_0f0cdeee6c9bf3d7 | Italian/French | Hyogo-ken Kobe-shi | 34.695124 | 135.197852 |
| 1 | air_7cc17a324ae5c7dc | Italian/French | Hyogo-ken Kobe-shi | 34.695124 | 135.197852 |
| 2 | air_fee8dcf4d619598e | Italian/French | Hyogo-ken Kobe-shi | 34.695124 | 135.197852 |
# 棒グラフで描画 df2_air_area_name = df2_city.groupby('air_area_name').size().sort_values() plt.figure(figsize=(12, 14)) plt.barh(np.arange(1,56), df2_air_area_name.values, tick_label=df2_air_area_name.index, align="center", color='aqua') plt.title("air_genre_freq") plt.xlabel("frequency") plt.ylabel("genre") plt.grid(True)
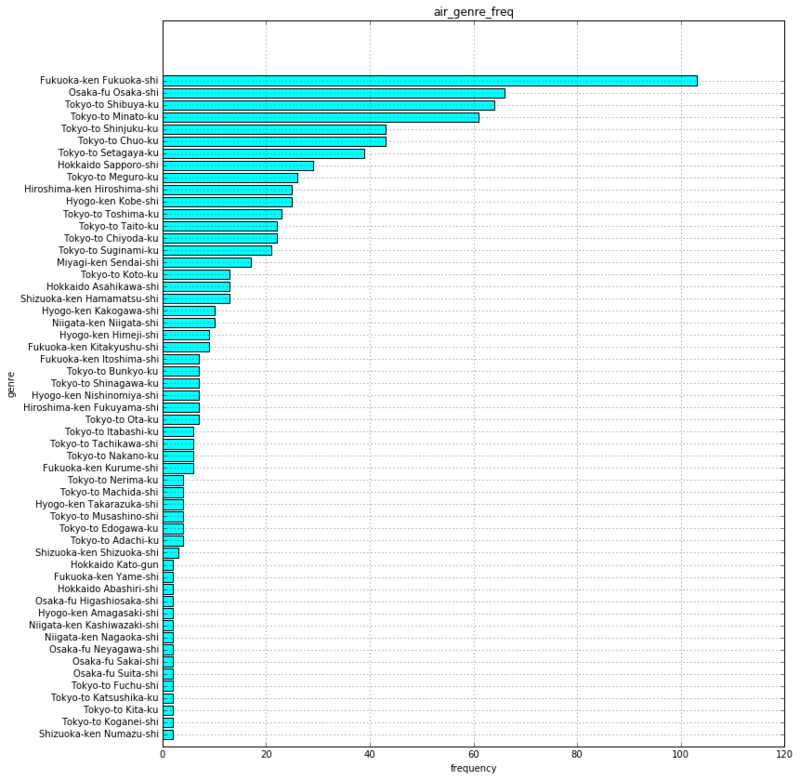
3−2−2.都道府県ごとの店舗数
# エリアを都道府県レベルに変更 df2_pref = df2_city.copy() df2_pref['air_area_name'] = df2_pref.air_area_name.map(lambda x: ' '.join(x.split(' ')[:1])) df2_pref.head(3)
| air_store_id | air_genre_name | air_area_name | latitude | longitude | |
|---|---|---|---|---|---|
| 0 | air_0f0cdeee6c9bf3d7 | Italian/French | Hyogo-ken | 34.695124 | 135.197852 |
| 1 | air_7cc17a324ae5c7dc | Italian/French | Hyogo-ken | 34.695124 | 135.197852 |
| 2 | air_fee8dcf4d619598e | Italian/French | Hyogo-ken | 34.695124 | 135.197852 |
# 棒グラフで描画 df2_air_area_name = df2_pref.groupby('air_area_name').size().sort_values() plt.barh(np.arange(1,10), df2_air_area_name.values, tick_label=df2_air_area_name.index, align="center", color='aqua') plt.title("air_genre_freq") plt.xlabel("frequency") plt.ylabel("genre") plt.grid(True)
3−3.エリア x ジャンルの分布
# データフレームをピボット df2_pref_heat = pd.pivot_table(data=df2_pref, values='air_store_id', columns='air_area_name', index='air_genre_name', aggfunc='count').sort_values(by='Tokyo-to',ascending=False) df2_pref_heat = df2_pref_heat.T.sort_values(by='Izakaya',ascending=False) df2_pref_heat.head(3)
| air_genre_name | Cafe/Sweets | Izakaya | Dining bar | Italian/French | Bar/Cocktail | Japanese food | Other | Western food | Creative cuisine | Okonomiyaki/Monja/Teppanyaki | Yakiniku/Korean food | Asian | International cuisine | Karaoke/Party |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| air_area_name | ||||||||||||||
| Tokyo-to | 87.0 | 87.0 | 65.0 | 65.0 | 54.0 | 38.0 | 16.0 | 14.0 | 5.0 | 5.0 | 4.0 | 2.0 | 2.0 | NaN |
| Fukuoka-ken | 45.0 | 27.0 | 14.0 | 11.0 | 9.0 | 11.0 | 5.0 | NaN | 2.0 | NaN | 3.0 | NaN | NaN | NaN |
| Hyogo-ken | 10.0 | 24.0 | 4.0 | 9.0 | NaN | 2.0 | NaN | NaN | 4.0 | 2.0 | 2.0 | NaN | NaN | NaN |
# ヒートマップを描画 plt.figure(figsize=(8, 4)) sns.heatmap(df2_pref_heat, annot=True, center=30, fmt='g', cmap='Blues')
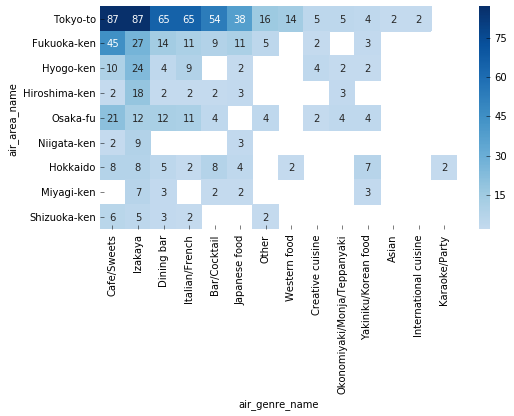
3–4.気づき
ジャンル x エリアの分布に規則性が見られる
- 何らかのルールでサンプリングされていそう
4.hpg_reserve.csv [ホットペッパーグルメの予約データ]
- 2,000,320レコード
- 13,325 /4,690店舗の予約データ???
- 訪問予定は、2016-01-01 11:00:00 〜 2017-05-31 23:00:00
- 予約時刻は、2016-01-01 00:00:00 〜 2017-04-22 23:00:00
# .csvをDataFrame化 df4 = pd.read_csv('Data/csv/hpg_reserve.csv') df4.head(3)
| hpg_store_id | visit_datetime | reserve_datetime | reserve_visitors | |
|---|---|---|---|---|
| 0 | hpg_c63f6f42e088e50f | 2016-01-01 11:00:00 | 2016-01-01 09:00:00 | 1 |
| 1 | hpg_dac72789163a3f47 | 2016-01-01 13:00:00 | 2016-01-01 06:00:00 | 3 |
| 2 | hpg_c8e24dcf51ca1eb5 | 2016-01-01 16:00:00 | 2016-01-01 14:00:00 | 2 |
# データ型を確認
df4.dtypes
hpg_store_id object
visit_datetime object
reserve_datetime object
reserve_visitors int64
dtype: object
# データ型を修正 df4['visit_datetime'] = df4.visit_datetime.map(lambda x: datetime.strptime(x,'%Y-%m-%d %H:%M:%S')) df4['reserve_datetime'] = df4.reserve_datetime.map(lambda x: datetime.strptime(x,'%Y-%m-%d %H:%M:%S')) df4.dtypes
hpg_store_id object
visit_datetime datetime64[ns]
reserve_datetime datetime64[ns]
reserve_visitors int64
dtype: object
# 統計量を確認 df4.describe(include='all')
| hpg_store_id | visit_datetime | reserve_datetime | reserve_visitors | |
|---|---|---|---|---|
| count | 2000320 | 2000320 | 2000320 | 2.000320e+06 |
| unique | 13325 | 9847 | 11450 | NaN |
| top | hpg_2afd5b187409eeb4 | 2016-12-16 19:00:00 | 2016-12-12 21:00:00 | NaN |
| freq | 1155 | 10528 | 907 | NaN |
| first | NaN | 2016-01-01 11:00:00 | 2016-01-01 00:00:00 | NaN |
| last | NaN | 2017-05-31 23:00:00 | 2017-04-22 23:00:00 | NaN |
| mean | NaN | NaN | NaN | 5.073785e+00 |
| std | NaN | NaN | NaN | 5.416172e+00 |
| min | NaN | NaN | NaN | 1.000000e+00 |
| 25% | NaN | NaN | NaN | 2.000000e+00 |
| 50% | NaN | NaN | NaN | 3.000000e+00 |
| 75% | NaN | NaN | NaN | 6.000000e+00 |
| max | NaN | NaN | NaN | 1.000000e+02 |
4−1.月間予約数
# 予約数を月次で集計 df4_monthly = df4.copy() df4_monthly['reserve_datetime'] = df4_monthly.reserve_datetime.map(lambda x: x.strftime('%Y-%m')) drop_col = ['hpg_store_id','visit_datetime'] df4_monthly = df4_monthly.rename(columns={'reserve_datetime': 'reserve_month'}).drop(drop_col,axis=1) df4_monthly = df4_monthly.groupby(['reserve_month']).count().reset_index().rename(columns={'reserve_visitors':'reserve'}) df4_monthly.head(3)
| reserve_month | reserve | |
|---|---|---|
| 0 | 2016-01 | 80905 |
| 1 | 2016-02 | 79934 |
| 2 | 2016-03 | 98276 |
# 棒グラフで描画 plt.figure(figsize=(14, 8)) plt.bar(np.arange(1,17), df4_monthly.reserve.as_matrix(), tick_label=df4_monthly.reserve_month, align="center", color='pink') plt.title("Monthly_hpg_reserve") plt.xticks(rotation = 30) plt.xlabel("month") plt.ylabel("reserve") plt.grid(True)
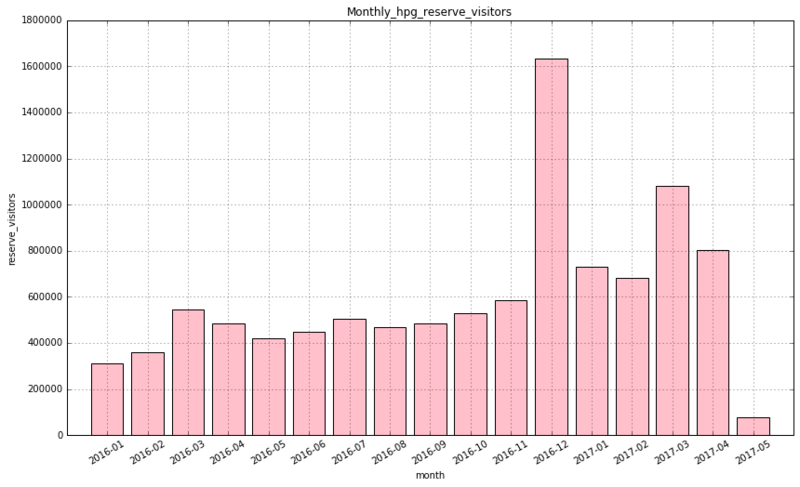
4−2.月別訪問予定者数
# 訪問予定者数を月次で集計 df4_monthly = df4.copy() df4_monthly['visit_datetime'] = df4_monthly.visit_datetime.map(lambda x: x.strftime('%Y-%m')) drop_col = ['hpg_store_id','reserve_datetime'] df4_monthly = df4_monthly.rename(columns={'visit_datetime': 'visit_month'}).drop(drop_col,axis=1) df4_monthly = df4_monthly.groupby(['visit_month'])['reserve_visitors'].sum().reset_index() df4_monthly.head(3)
| visit_month | reserve_visitors | |
|---|---|---|
| 0 | 2016-01 | 313180 |
| 1 | 2016-02 | 359597 |
| 2 | 2016-03 | 546433 |
# 棒グラフで描画 plt.figure(figsize=(14, 8)) plt.bar(np.arange(1,18), df4_monthly.reserve_visitors.as_matrix(), tick_label=df4_monthly.visit_month, align="center", color='pink') plt.title("Monthly_hpg_reserve_visitors") plt.xticks(rotation = 30) plt.xlabel("month") plt.ylabel("reserve_visitors") plt.grid(True)
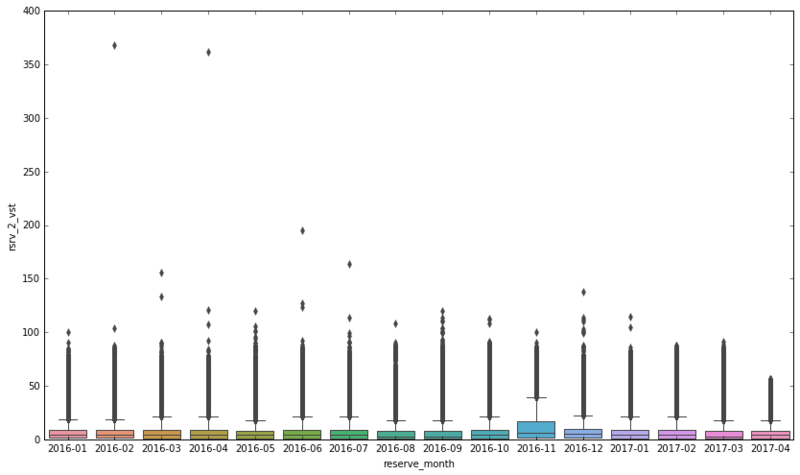
4−3.予約日から訪問予定日までの日数
# 予約日から訪問予定日までの日数を追加 df4_monthly = df4.copy() df4_monthly['rsrv_2_vst'] = df4_monthly.visit_datetime - df4_monthly.reserve_datetime df4_monthly['rsrv_2_vst'] = df4_monthly.rsrv_2_vst.map(lambda x: x.days) df4_monthly['reserve_datetime'] = df4_monthly.reserve_datetime.map(lambda x: x.strftime('%Y-%m')) df4_monthly = df4_monthly.rename(columns={'reserve_datetime': 'reserve_month'}) df4_monthly.tail(3)
| hpg_store_id | visit_datetime | reserve_month | reserve_visitors | rsrv_2_vst | |
|---|---|---|---|---|---|
| 2000317 | hpg_e9151de687b93aa3 | 2017-05-31 21:00:00 | 2017-04 | 49 | 47 |
| 2000318 | hpg_fae6c96189b4a122 | 2017-05-31 21:00:00 | 2017-04 | 9 | 42 |
| 2000319 | hpg_0b70de808b55ad1e | 2017-05-31 23:00:00 | 2017-04 | 6 | 40 |
plt.figure(figsize=(14, 8)) sns.boxplot(x="reserve_month", y="rsrv_2_vst", data=df4_monthly)

4−4.気づき
2016年10月以降のデータ量が多い
- 純粋な増加なのか、データ収集基盤の改善か、サンプリングによるものかは不明
11月の予約から訪問までの日差は大きい
- 忘年会に備えた事前予約数が多い
5.hpg_store_info.csv [ホットペッパーグルメのレストラン情報]
- 4,690の店舗データ
- 34ジャンル
- 119エリア
# .csvをDataFrame化 df5 = pd.read_csv('Data/csv/hpg_store_info.csv') df5.head(3)
| hpg_store_id | hpg_genre_name | hpg_area_name | latitude | longitude | |
|---|---|---|---|---|---|
| 0 | hpg_6622b62385aec8bf | Japanese style | Tōkyō-to Setagaya-ku Taishidō | 35.643675 | 139.668221 |
| 1 | hpg_e9e068dd49c5fa00 | Japanese style | Tōkyō-to Setagaya-ku Taishidō | 35.643675 | 139.668221 |
| 2 | hpg_2976f7acb4b3a3bc | Japanese style | Tōkyō-to Setagaya-ku Taishidō | 35.643675 | 139.668221 |
# データ型を確認
df5.dtypes
hpg_store_id object
hpg_genre_name object
hpg_area_name object
latitude float64
longitude float64
dtype: object
# 統計量を確認 df5.describe(include='all')
| hpg_store_id | hpg_genre_name | hpg_area_name | latitude | longitude | |
|---|---|---|---|---|---|
| count | 4690 | 4690 | 4690 | 4690.000000 | 4690.000000 |
| unique | 4690 | 34 | 119 | NaN | NaN |
| top | hpg_b6fcb5aea05b867b | Japanese style | Tōkyō-to Shinjuku-ku None | NaN | NaN |
| freq | 1 | 1750 | 257 | NaN | NaN |
| mean | NaN | NaN | NaN | 35.810261 | 137.675816 |
| std | NaN | NaN | NaN | 2.138755 | 3.197233 |
| min | NaN | NaN | NaN | 33.311645 | 130.339313 |
| 25% | NaN | NaN | NaN | 34.692109 | 135.498859 |
| 50% | NaN | NaN | NaN | 35.659214 | 139.495733 |
| 75% | NaN | NaN | NaN | 35.703381 | 139.737998 |
| max | NaN | NaN | NaN | 43.774846 | 143.714585 |
5−1.ジャンルごとの店舗数
# ジャンルの内訳と頻度 df5.groupby('hpg_genre_name').size().sort_values(ascending=False).describe()
count 34.000000
mean 137.941176
std 323.163055
min 1.000000
25% 5.000000
50% 25.500000
75% 79.750000
max 1750.000000
dtype: float64
# 棒グラフで描画 df5_hpg_genre_name = df5.groupby('hpg_genre_name').size().sort_values() plt.figure(figsize=(8, 10)) plt.barh(np.arange(1,35), df5_hpg_genre_name.values, tick_label=df5_hpg_genre_name.index, align="center", color='orange') plt.title("hpg_genre_freq") plt.xlabel("frequency") plt.ylabel("genre") plt.grid(True)
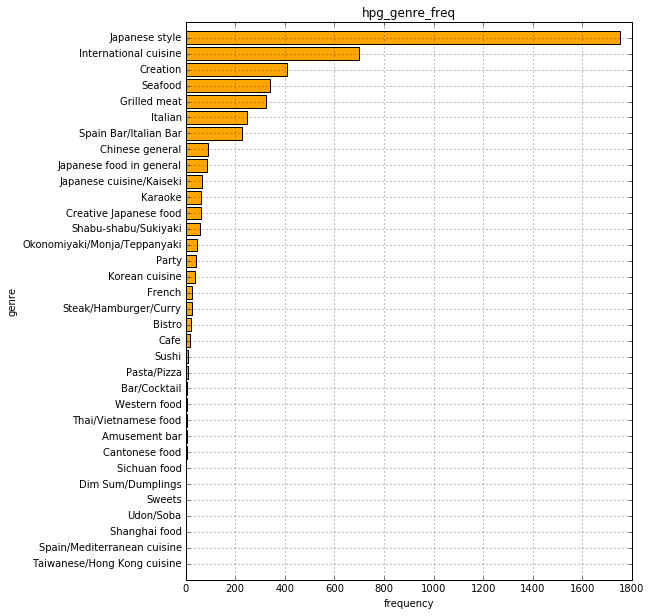
5−2.エリアごとの店舗数
# エリアの内訳と頻度 df5.groupby('hpg_area_name').size().sort_values(ascending=False).describe()
count 119.000000
mean 39.411765
std 45.887004
min 1.000000
25% 8.000000
50% 20.000000
75% 58.000000
max 257.000000
dtype: float64
5−2−1.市区町村ごとの店舗数
# エリアを市区町村レベルに変更、plot時の文字化け対策で置換 df5_city = df5.copy() df5_city['hpg_area_name'] = df5_city.hpg_area_name.map(lambda x: ' '.join(x.split(' ')[:2]).translate(str.maketrans('Ōōū', 'Oou'))) df5_city.head(3)
| hpg_store_id | hpg_genre_name | hpg_area_name | latitude | longitude | |
|---|---|---|---|---|---|
| 0 | hpg_6622b62385aec8bf | Japanese style | Tokyo-to Setagaya-ku | 35.643675 | 139.668221 |
| 1 | hpg_e9e068dd49c5fa00 | Japanese style | Tokyo-to Setagaya-ku | 35.643675 | 139.668221 |
| 2 | hpg_2976f7acb4b3a3bc | Japanese style | Tokyo-to Setagaya-ku | 35.643675 | 139.668221 |
# 棒グラフで描画 df5_hpg_area_name = df5_city.groupby('hpg_area_name').size().sort_values() plt.figure(figsize=(12, 22)) plt.barh(np.arange(1,74), df5_hpg_area_name.values, tick_label=df5_hpg_area_name.index, align="center", color='yellow') plt.title("hpg_genre_freq") plt.xlabel("frequency") plt.ylabel("genre") plt.grid(True)
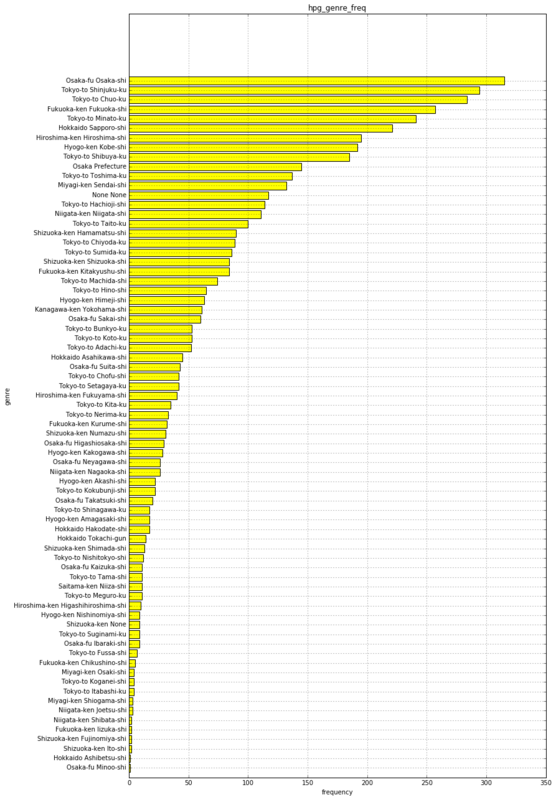
5−2−2.都道府県ごとの店舗数
# エリアを都道府県レベルに変更 df5_pref = df5_city.copy() df5_pref['hpg_area_name'] = df5_pref.hpg_area_name.map(lambda x: ' '.join(x.split(' ')[:1])) df5_pref.head(3)
| hpg_store_id | hpg_genre_name | hpg_area_name | latitude | longitude | |
|---|---|---|---|---|---|
| 0 | hpg_6622b62385aec8bf | Japanese style | Tokyo-to | 35.643675 | 139.668221 |
| 1 | hpg_e9e068dd49c5fa00 | Japanese style | Tokyo-to | 35.643675 | 139.668221 |
| 2 | hpg_2976f7acb4b3a3bc | Japanese style | Tokyo-to | 35.643675 | 139.668221 |
# 棒グラフで描画 df5_hpg_area_name = df5_pref.groupby('hpg_area_name').size().sort_values() plt.barh(np.arange(1,14), df5_hpg_area_name.values, tick_label=df5_hpg_area_name.index, align="center", color='yellow') plt.title("hpg_genre_freq") plt.xlabel("frequency") plt.ylabel("genre") plt.grid(True)
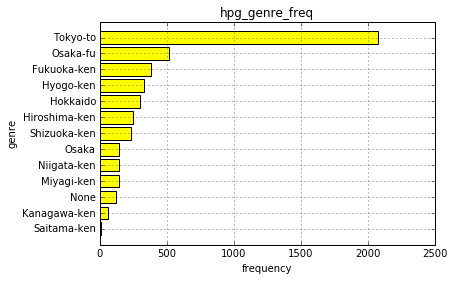
5−3.エリア x ジャンルの分布
# データフレームをピボット df5_pref_heat = pd.pivot_table(data=df5_pref, values='hpg_store_id', columns='hpg_area_name', index='hpg_genre_name', aggfunc='count').sort_values(by='Tokyo-to',ascending=False) df5_pref_heat = df5_pref_heat.T.sort_values(by='Japanese style',ascending=False) df5_pref_heat.head()
| hpg_genre_name | Japanese style | International cuisine | Creation | Seafood | Grilled meat | Italian | Spain Bar/Italian Bar | Chinese general | Karaoke | Korean cuisine | ... | Dim Sum/Dumplings | Spain/Mediterranean cuisine | Sushi | Sweets | Taiwanese/Hong Kong cuisine | Western food | Amusement bar | Bar/Cocktail | Cantonese food | Udon/Soba |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| hpg_area_name | |||||||||||||||||||||
| Tokyo-to | 805.0 | 370.0 | 152.0 | 121.0 | 118.0 | 116.0 | 109.0 | 45.0 | 28.0 | 27.0 | ... | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | NaN | NaN | NaN | NaN |
| Osaka-fu | 196.0 | 44.0 | 63.0 | 35.0 | 57.0 | 36.0 | 23.0 | 9.0 | 3.0 | 4.0 | ... | NaN | NaN | 1.0 | 1.0 | NaN | 1.0 | NaN | NaN | NaN | NaN |
| Fukuoka-ken | 143.0 | 65.0 | 42.0 | 32.0 | 41.0 | 19.0 | 18.0 | 4.0 | 2.0 | NaN | ... | NaN | NaN | 1.0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| Hyogo-ken | 106.0 | 29.0 | 30.0 | 24.0 | 35.0 | 13.0 | 8.0 | 13.0 | 1.0 | 4.0 | ... | NaN | NaN | 1.0 | NaN | NaN | 1.0 | NaN | 1.0 | 4.0 | NaN |
| Shizuoka-ken | 92.0 | 32.0 | 22.0 | 24.0 | 7.0 | 10.0 | 11.0 | 3.0 | 2.0 | NaN | ... | NaN | NaN | 4.0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
5 rows × 34 columns
# ヒートマップを描画 plt.figure(figsize=(18, 6)) sns.heatmap(df5_pref_heat, annot=True, fmt='g', center=300, cmap='Oranges')

5–4.気づき
サンプリングされているとして、均一に取られていそう
- ランダムにサンプリングか
6.store_id_relation.csv [id横断データ]
- 150店舗、1対1
# .csvをDataFrame化 df7 = pd.read_csv('Data/csv/store_id_relation.csv') df7.head(3)
| air_store_id | hpg_store_id | |
|---|---|---|
| 0 | air_63b13c56b7201bd9 | hpg_4bc649e72e2a239a |
| 1 | air_a24bf50c3e90d583 | hpg_c34b496d0305a809 |
| 2 | air_c7f78b4f3cba33ff | hpg_cd8ae0d9bbd58ff9 |
# データ型を確認
df7.dtypes
air_store_id object
hpg_store_id object
dtype: object
# 統計量を確認
df7.describe()
| air_store_id | hpg_store_id | |
|---|---|---|
| count | 150 | 150 |
| unique | 150 | 150 |
| top | air_622375b4815cf5cb | hpg_eaa312b3100ae94b |
| freq | 1 | 1 |
7.date_info.csv [カレンダー]
- 2016-01-01〜2017-05-31
# .csvをDataFrame化 df6 = pd.read_csv('Data/csv/date_info.csv') df6.head(3)
| calendar_date | day_of_week | holiday_flg | |
|---|---|---|---|
| 0 | 2016-01-01 | Friday | 1 |
| 1 | 2016-01-02 | Saturday | 1 |
| 2 | 2016-01-03 | Sunday | 1 |
# データ型を確認
df6.dtypes
calendar_date object
day_of_week object
holiday_flg int64
dtype: object
# データ型を修正 df6['calendar_date'] = df6.calendar_date.map(lambda x: datetime.strptime(x,'%Y-%m-%d')) df6.dtypes
calendar_date datetime64[ns]
day_of_week object
holiday_flg int64
dtype: object
# 統計量を確認 df6.describe(include='all')
| calendar_date | day_of_week | holiday_flg | |
|---|---|---|---|
| count | 517 | 517 | 517.000000 |
| unique | 517 | 7 | NaN |
| top | 2016-09-08 00:00:00 | Sunday | NaN |
| freq | 1 | 74 | NaN |
| first | 2016-01-01 00:00:00 | NaN | NaN |
| last | 2017-05-31 00:00:00 | NaN | NaN |
| mean | NaN | NaN | 0.067698 |
| std | NaN | NaN | 0.251471 |
| min | NaN | NaN | 0.000000 |
| 25% | NaN | NaN | 0.000000 |
| 50% | NaN | NaN | 0.000000 |
| 75% | NaN | NaN | 0.000000 |
| max | NaN | NaN | 1.000000 |
続きはこちら
転職してからこれまでを振り返る

9月に書いたこちらの記事を振り返りつつ、これからを考える記事。日記の域をでず、アイキャッチ画像には何の意味もない。
select-from-where.hatenablog.com
9月から今までの話
未だにデータマートを拵えおじさんをやっている
前回の転職後エントリから半年が経過した。 常駐先では急な天変地異により自社メンバーが私1人になり、孤軍奮闘の後、他社パートナーの方を迎え(たのはあくまでクライアントなのだが、)日常業務を平常運転で消化できるようになってきた。
業務内容はというと、相変わらずデータマートの開発、保守・運用。時々スポットでデータ抽出・加工するなどしている。 主にSQLを用いてBIツールで参照するためのマートを作成、モニタリング環境にデプロイする。既存のマートの改修依頼も多く、新規案件も請け負いながら、保守案件もこなすといった日々を送っている。
そのため、業務時間中にじっくりとデータ分析をすることはない。入社時の肩書き「データアナリスト」を(個人的に)捨て、最近はデータエンジニアとかBI開発エンジニアと名乗るようにしているし、Twitterの肩書きも書き変えた(涙目)
私はただ降りてくる仕事をこなしているだけなのか?
業務委託の立場ではあるが、あるサービスのモニタリング基盤担当窓口として、クライアントのプロパー社員を介さずに要件のヒアリング、設計から携わることができている。現場にノウハウを持った人間がおらず、この設計で良い分析ができるのか?と日々疑問を感じながらではあるが、知識をつけたり、試行錯誤しながら、少しづつ手応えを掴みつつある。
誰かに指示を受けることもマネジメントされることもないため、まるでフリーランスエンジニアのようだと感じている。
私なりに前任者から引き継いだ業務フローには存在しない仕事に取り組んできた。 個人のキャリア形成やスキルアップと組織貢献を天秤にかけたとき、組織貢献をとりたくなる性格だ。(この職で長く食っていくにはまあまあ危険な属性であることは自覚している。) そのためか組織の抱える課題が目につき、やりたいことでなくても、ポータブルスキルを磨くことにならなくても、できるところからどうにかしてやりたいと考えて取り組んできたつもりだ。
だから私は、ただ降りてくる仕事をこなすだけで日々を過ごしてはいないと思う。でも物足りない、意思決定をしていないし、意思決定を支援しているという実感も薄い。
私の考える組織が抱える課題とは
今の現場は、高速な処理基盤を手に入れ、モダンなBIツール導入のスモールスタートに成功していたものの、様々な問題を抱えていた。解消していないものもまだまだある。
下記に少しだけ具体的にあげたくて一度は書いたのだが、身分も勤め先も明かしていないとはいえリテラシー的に問題ありすぎるので非公開。(BI活用のアンチパターンになる気がするので、これだけで記事書いてみたいと思ったりもするが。)
私が取り組んだこと
1. データマートの作成・改修依頼から開発、デプロイまでの業務フロー策定
何としても新規参入者が来る前に手を打ちたかった。具体的にやったことは3つ。ノウハウがあったわけではないので、現在も運用しながら改善を加えている最中だ。
- 依頼フローの整備 依頼者側の窓口を集約し、依頼時のフォーマット作成を支援した。 また、要件定義の1次チェックを依頼者側の窓口に寄せることで、要件定義にかかる工数を削減した。
- 開発フローの作成、明示 開発工程を具体化し、必要工数の目安を開示して、依頼者側の窓口と認識を合わせた。 また、プロジェクト管理ツールの運用ルールを策定した。
- 諸々手順書の作成 これは新規参画者への引継ぎのためでもあった。 具体的に何するコマンドとオプションかわからないけど、どういう結果になるかはわかるからそのままやればいいんでしょ的な使われ方になりがちである事を意識しつつ、作業の意図と合わせて明文化する事を心がけた。
2. 大枠の設計概念の策定と明文化
開発フローの作成にも大きく関わるのだが、利用者が多くもはや潰すことのできないマートを維持しつつ、保守にかかる工数が軽減されるような設計概念を明文化して依頼者側の窓口と共有した。
具体的には、可能な限りスタースキーマの概念に沿うよう既存のデータマートを取り込んだ設計概念を固め、作成依頼に基づかないディメンションテーブルの拡充作業を独自に進めた。これにより頻発していたディメンション追加依頼の削減につながることを期待したが、ファクトテーブルが不足していることもあって開発依頼は絶えない
3. データマートの仕様に関するドキュメントを拡充
一応存在していたテーブル定義書(誤植多...)をベースに、既存のSQLを解析してドキュメントを整備、公開した。とは言っても、ドキュメント不足の解消には至っておらず、まだまだ拡充が必要だと感じている。
なんとか「同じ指標でも部署によってデータ抽出方法が方法が異なり、せっかくのBI基盤が組織横断の共通言語となっていない」状態を解消していきたい。
そのほか
- 他社パートナーとうまく付き合うこと
現在他社パートナーのメンバーとタッグを組んで業務にあたっている。
同じ組織の仲間であるという事を強く意識して接している。現職について1年も満たない私の知見ではあるが、全てオープンにして密にコミュニケーションを取るようにしている。
チャットやミーティングで業務に限らない情報を連携し続けた事で、相手からも情報が飛んで来るようになった。実感的には良好な関係を築くことができている。
環境面の変化
当然だが、環境面も大きく変化したのでその影響をざっくりまとめてみる
●よくなった
- (前職と比べると)比較的モダンなシステム環境や、ツールに触れることができる
- 学ぶ意欲と就労への活力を感じるようになった
- 自己研鑽に割く気力と時間ができた
- 業務時間中にじっくり思考して、作業に没頭できる時間ができた
- コミュニケーションコストが下がった(チャットやプロジェクト管理ツール、ペーパーレス)
- 年功序列の給与体系から脱却した
×悪くなった
- (前職と比べると)チームらしいチームで仕事していない
- プロジェクト単位の総工数が小さい(25〜30人月→3〜20人日)
- 一時的な年収の下落
- (前職と比べると)休みが取りづらい(意図的に取れる長期休暇がない)
これまでに身につけたこと
そんなこんなでなんとかやってきたわけだが、ここまでで身についたポータブルスキルを「テクニカル」「ヒューマン」に分けて整理してみた。
テクニカル:仕事や業務を適切にこなす能力(業務遂行能力)
●ある程度できている
- SQL(Hive,BigQuery)を不自由なく自在に操る
- 業務システムに蓄積されている正規化されたデータのETL
- Hadoop、GCP(BigQuery,CloudStrage,CloudShell)を駆使したデータのETL
- 最低限のプログラミング(Python,Linux(ShellScript))
- BIツール(Tableau)の操作
- クライアントのビジネスモデル理解
- データ分析向け要件定義力
- 保守性を考慮した運用設計
- モニタリング基盤の運用(インフラは除く)
×できるようにならねば...
- クライアントの属する業界動向のウォッチ
- Google Analytics等アクセス解析の知識
ヒューマン:人間関係を円滑にし、人との繋がりを最大限に活用する能力(対人関係能力)
●ある程度できている
- 業務委託としての領分をわきまえた業務遂行(これ大事...)
- 同じ領域を担う他社パートナーとの関係構築
- 業務の枠を超えた個人的な取り組み
- 個人の責任が重く、プロ意識が向上した
×できるようにならねば...
- コネクションを増やすための社外活動(今月から活発にやっていたりはする)
個人の課題とこれから取り組みたいこと
スキルセットと環境の面から考えてみる。 様々な企業の募集要項を眺めて作成してみたが、到底やりきれないので、同業とのネットワークを作りつつ、自分が優先的に専門性を高めるべき箇所を見極めたい
▲自分に足りていないスキル
- 半年〜1年でできる
- 3年かかる
- もっと長期的に見るべき
- 機械学習や分析結果を用いたサービスモデルの開発
×今の環境ではできそうにないこと
- 自社サービスの発展に貢献する
- ユーザーに価値を届けることに貢献する
- 自ら組織を横断してコミュニケーションを取り、データを収集して分析する
- 組織の目標を意識し、チームワークを駆使して業務を遂行する
これから大切にして行きたいこと
夢を再確認したい。私が社会人として実現したいことは二つある。
1.情緒的な満足感をユーザに提供するサービスに携わりたい
これは絶対に夢のままで終わらせたくない。
自分の仕事が誰かの生活を少しでも豊かにしていると信じて働けるのは幸せなはずだ。とか未だに夢を見ている。
2.データを組織横断の共通言語にし、データ活用を普及・促進させる組織を作りたい
人の入れ替わりが激しい業界だと思うが、私は結局、組織を重視して物事を見て考えるタイプだ。
どこがうまく行っていないか、軌道修正すべきかを観察して気づくことができる。
エンジニアリング力をとっても、データ分析力をとっても、今から尖った人材になるのは難しそうだ。しかし、組織を俯瞰してみる力には自信があって、自分の強みだと考えている(成果として提示することは難しいが...)
だから、様々な能力を持つ人たちが集まり、その力を発揮できるような組織を率いる人間になりたい。
そのために一つ、これは負けんという専門性の高さを身に付けたい。まだまだ低いレベルにいるビジネスも、テクノロジーに関する知識も、マネジメント力も自信が芽生えるようになるまで引き上げていきたい。
そして何より、それらを実現することができそうな環境を掴み取りたい。
ランディングページ (Landing Page, LP) とはなんたるか
仕事ではないのだけど、ランディングページの作成に取り組むことになった。
Webに関する知識がとにかく乏しい。。ということで、まずランディングページとはなんたるかを調べてみた。
メモ書きをGistで公開しています。
LandingPage.md · GitHub
ランディングページ(Landing Page, LP)
広義のランディングページ
ユーザがサイトへの流入時に最初にアクセスしたページ
つまり、Web上で公開されている全てのページはランディングページとなりうる。
アクセス解析をする場合は、こちらの意味で使用することが多い。
狭義のランディングページ
ユーザをダイレクトにアクション(注文、問い合わせなど)に結びつけることを目的としたページ
広告施策用に制作する1ページで完結する縦長のページ
リスティング広告で施策を打つ場合、検索ワードに応じて複数のLPを用意することがある
この記事では、狭義のランディングページについて整理しています。
LPの持つ特徴
下記は、商品・サービスの『特性』や『目的』に応じて持たせる特徴を工夫する必要がある
- 縦に長いページ構成
ユーザに検索の手間を取らせないよう、情報を詰め込んでいる
≒ 営業トーク。ユーザが欲しい情報を、売り手が見せたい順番で提供できる - リンクが少ない
コンバージョンを目的としているため、回遊性を下げ、直帰率を抑えている
≒ うまく作らないと、直帰率がかなり上がる - デザインの自由度が高い
グローバルナビゲーションや、サイドメニューが必要ない - ページあたりの作成コストは高い
原稿、デザインにかかる人件費、スマホ対応 - SEOと比べると施策的には低コスト
ランディングページ最適化(Landing Page Optimization, LPO)により、コンバージョンを向上
⇨ 同じの流入量でも売上を向上させることが可能、SEOよりも先に打つべき施策 - SEOに弱い
視覚的なインパクトを優先することから画像が多くなりがち
文字情報が少なくなり、画像読込みにより表示速度が遅くなる
⇨ SEOを気にせずにデザインできるという解釈もできる
LPの構成要素
物理的な構成要素
- ファーストビュー
要素:キャッチコピー・画像・コンバージョンボタンなど - ボディ
要素:メリット、製品・商品の具体的な情報、メディア掲載、利用者の声など - クロージング
要素:期間限定、プレゼント、サンプル提供、送料無料など
論理的な構成要素
論理的な構成にはいくつかのフレームワークが存在している
BEAF
- Benefit(ベネフィット)
ユーザにとってのメリット - Evidence(エビデンス)
メリットの根拠 - Advantage(アドバンテージ)
競合に対する優位性 - Feature(フィーチャー)
特徴、スペック
AIDA
- Attention(注意)
ユーザに響く画像やキャッチコピーで注意を引く - Interest(関心)
ユーザに具体的な説明で商品・サービスを訴求する - Desire(欲求)
ユーザにとってのメリットを伝え、欲求を掻き立てる - Action(行動)
ユーザをコンバージョンに結びつける動機付け
QUEST FORMULA
- Qualify(ターゲティング)
どのようなユーザにとってのソリューションであるかを明示することで対象を絞り込む - Understand(理解・共感)
ユーザへの理解を示し、共感を表明することで信頼感を与える - Educate(教育)
ユーザに商品・サービスについての情報を提示し、信憑性を高めながら価値を伝える - Stimulate(興奮)
ユーザに商品・サービスを手にした後の効果や満足感を想像させる - Transition(行動)
ユーザがどのようなアクションを起こせば商品やサービスを手にできるのかを明示し、行動させる
LPO(Landing Page Optimization、ランディングページ最適化)
- ヒートマップツールの導入によるユーザの行動の把握
- フレームワークによる構成の見直し
- 心理学や人間工学、デザインの原則などに基づくデザインの見直し
- SEOによる流入からLPへ流し込む導線の作成
- リスティング広告のキーワードに応じた複数パターンのLP作成
参考にした記事
ds-b.jp
webkikaku.co.jp
webbu.jp
ferret-plus.com
liskul.com
kazuto-yoshida.com
webtan.impress.co.jp
Seleniumでクローリングとスクレイピングを試す python
とにかく試して見るシリーズ第5弾。
前回、BeautifulSoupでスクレイピングを試したが、なんだかあまり活用する場面が思い浮かばんなあと思っていた。
同僚の方が普段使っているということで、手ほどきを受けながら挑戦した。
今回はソースコードの公開を控える(どっちみち酷いコードなのですが...)。
なぜやったのか
やっぱりpythonでできそうなことは試しておきたい。
Web系のデータが驚くほど馴染まなかったので、もっとWebを理解していきたい。
試してみたこと
ある商材のスペックと販売価格を取得する。
手順は下記の通り。
1. メーカー単位の商品一覧ページのURLをクローリングして取得する
2. 各メーカーの商品詳細ページのURLをクローリングして取得する
3. 全てやりたいところだが、1メーカーの全商品に絞ってスクレイピングして、目的のデータを取得する
苦労した処理
- ページネイションをクリックしながら遷移させる処理
execute_scriptメソッドで、javascriptを実行する - メーカー名、商品名の取得
置換処理も交えて対処 - 商品スペックの掲載位置が商品によって異なる
ロジック組んで回避 - カラム名称として使用する、ヘッダー行をhtmlから生成
スクリプトでやる必要は全くないが、pythonでやることにこだわってみた。